FlareOn11: Challenge 7 - fullspeed
Introduction
If you're new to FlareOn or haven't heard about it, FlareOn is an annual reverse-engineering CTF competition organized by Mandiant team. It's designed to challenge security enthusiasts, malware analysts, and reverse engineers with a series of increasingly difficult puzzles that test a wide range of skills, from binary analysis and deobfuscation to encryption and scripting. Each level is crafted to mimic real-world scenarios in malware analysis, providing participants with hands-on experience in tackling complex reverse-engineering tasks.
In this writeup, I'll walkthrough my solution for the 7th challenge of FlareOn 11.
In this challenge, we are asked to reverse engineer a .net program. However, it's not the typical format of .net programs that you can throw at dnSpy to get it decompiled. In this scenario, the program is a .net program that is Ahead-of-Time (AOT) compiled.
Ahead-of-Time (AOT) Compilation is a process where a program is compiled into machine code before it is executed, rather than being interpreted or compiled at runtime (as in Just-in-Time (JIT) compilation). In AOT, the source code (or an intermediate representation like bytecode) is compiled into native machine code for the target platform during the build process. This simply means that the .NET program written in C# has been compiled to native machine code.
Of course, the reverse engineering process of such programs are not so simple. Additionally, the challenge required some cryptography experience in order to break the encryption part of it. We'll go through each step in this walkthrough.
Walkthrough
This FlareOn 11 challenge reads as follows:
TITLE: fullspeed
Has this all been far too easy?
Where's the math? Where's the science?
Where's the, I don't know.... cryptography?
Well we don't know about any of that, but
here is a little .NET binary to chew on while you
discuss career changes with your life coach.
7zip archive password: flare
The challenge can be downloaded through the following file:
If you would like to download all FlareOn-11 challenges, you can download them from here.
First, after unzipping the challenge file, we take a look at the challenge files:

We are provided with binary file and a PCAP file containing the following traffic:
If we attempt to run the binary, we'll notice that it's trying to reach the service on port 31337 on the local IP 192.168.56.103.
The packet capture shows that the client (the endpoint running fullspeed.exe) sends two buffers of equal length and then expects two buffers in response. The first response buffer is the same length as the sent buffers, while the second is 7 bytes longer.
Due to the similar lengths, we can assume that this traffic can potentially be responsible for exchanging some data in order to initialize the communication.
Next, there are many other buffers exchanged of different lengths.
This is all that the capture.pcap has to offer. Now let's start the real work!
Upon loading this binary in IDA, we notice that the binary is stripped, and we lack information about most of the used functions.
Furthermore, inspecting strings in IDA shows some details about the environment and dependencies used when compiling the binary:
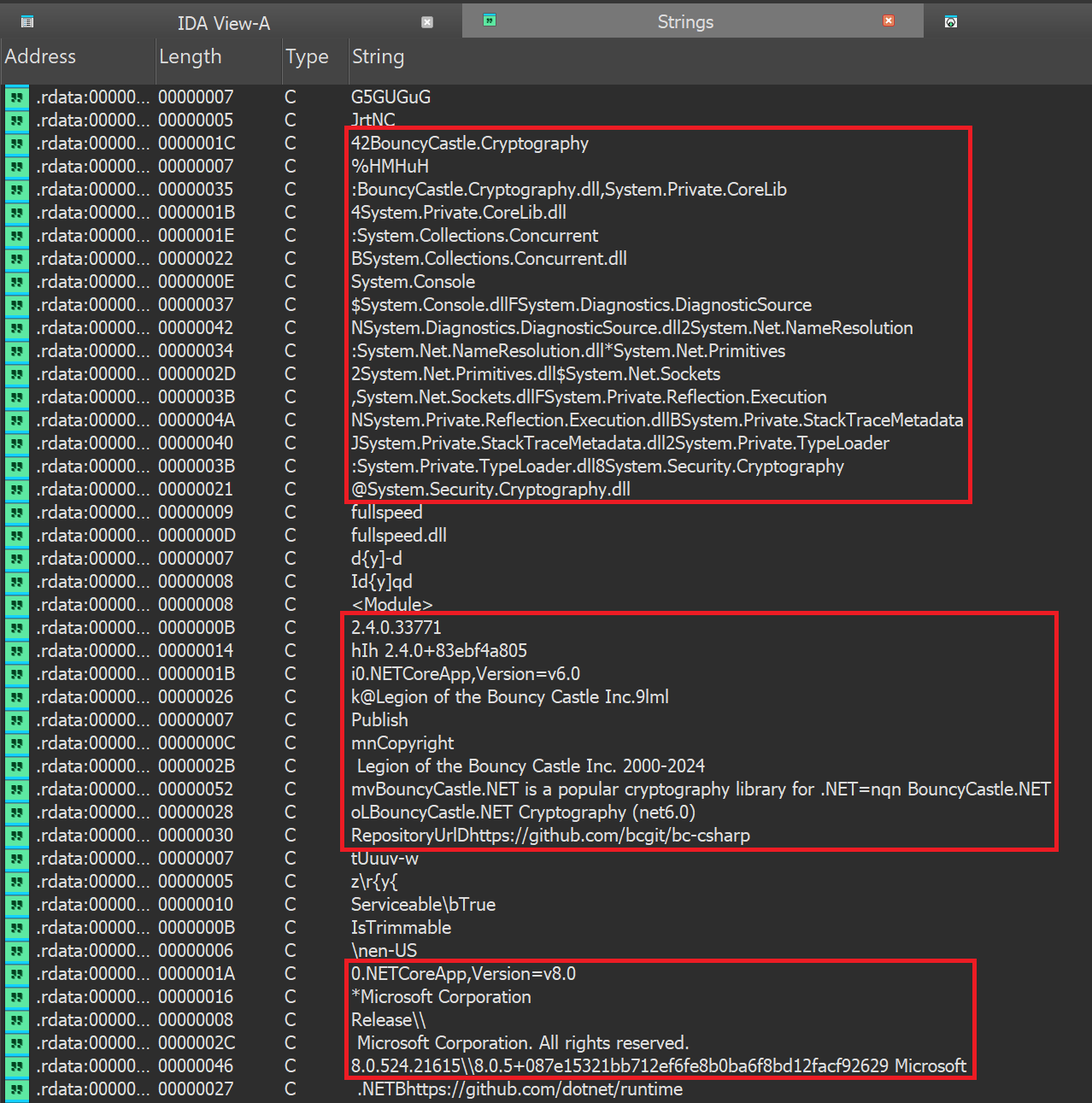
The strings indicate that the binary is a .NET Core application using several .NET runtime libraries, as well as the external cryptography library BouncyCastle. They also reveal the specific versions of the BouncyCastle library and the .NET runtime.
When you have a .NET application that is AOT compiled, the first step of reverse engineering it is to build FLIRT (Fast Library Identification and Recognition Technology) signature files.
These can be loaded in IDA in order to identify unknown library functions used in the binary.
One way to build these signature files is to compile a sample program with debugging symbols. This program must use the same libraries as the target binary. This way, we can produce a signature file from our binary and then import it in the target binary.
The more functions we identify, the easier our task becomes.
You can create a sample program, compile it with symbols, create a signature file, and then load it into our target binary.
For this challenge specifically, we'll likely need to create multiple .sig files. Each time you encounter a complex function, there's a high chance it's an unidentified library function.
To try to cover as much functions as we can, let's first attempt to compile and create a signature file for the same version of BouncyCastle library used in the challenge.
(base) joe@FlareVM:bouncycastle$ git clone https://github.com/bcgit/bc-csharp
Cloning into 'bc-csharp'...
...
(base) joe@FlareVM:bouncycastle$ cd bc-csharp/
(base) joe@FlareVM:bouncycastle$ git checkout 83ebf4a805
Updating files: 100% (602/602), done.
Note: switching to '83ebf4a805'.
...
HEAD is now at 83ebf4a8 Set version to '2.4'
Next, we'll update the .csproj file of the library stored in bc-csharp\crypto\src\BouncyCastle.Crypto.csproj in order to instruct the compiler to AOT compile the library:
<Project Sdk="Microsoft.NET.Sdk">
<PropertyGroup>
<TargetFrameworks>net8.0</TargetFrameworks>
<PublishAot>true</PublishAot>
<RootNamespace>Org.BouncyCastle</RootNamespace>
<AssemblyOriginatorKeyFile>..\..\BouncyCastle.NET.snk</AssemblyOriginatorKeyFile>
<SignAssembly>true</SignAssembly>
<NoWarn>1591</NoWarn>
<AssemblyName>BouncyCastle.Cryptography</AssemblyName>
<AssemblyTitle>BouncyCastle.NET Cryptography ($(TargetFramework))</AssemblyTitle>
<Authors>Legion of the Bouncy Castle Inc.</Authors>
<Company>Legion of the Bouncy Castle Inc.</Company>
<Copyright>Copyright © Legion of the Bouncy Castle Inc. 2000-2024</Copyright>
<Description>BouncyCastle.NET is a popular cryptography library for .NET</Description>
<PackageIcon>packageIcon.png</PackageIcon>
<PackageIconUrl>https://www.bouncycastle.org/stable/nuget/csharp/packageIcon.png</PackageIconUrl>
<PackageId>BouncyCastle.Cryptography</PackageId>
<PackageLicenseExpression>MIT</PackageLicenseExpression>
<PackageProjectUrl>https://www.bouncycastle.org/stable/nuget/csharp/website</PackageProjectUrl>
<PackageReadmeFile>README.md</PackageReadmeFile>
<PackageReleaseNotes>https://www.bouncycastle.org/stable/nuget/csharp/release_notes</PackageReleaseNotes>
<PackageTags>bouncycastle cryptography dtls encryption open-source openpgp post-quantum security tls</PackageTags>
<Product>BouncyCastle.NET</Product>
<PublishRepositoryUrl>true</PublishRepositoryUrl>
<Title>BouncyCastle.NET Cryptography</Title>
<Configurations>Debug;Release;Publish</Configurations>
</PropertyGroup>
<ItemGroup>
<TrimmerRootAssembly Include="BouncyCastle.Cryptography" />
</ItemGroup>
<PropertyGroup>
<EmbedUntrackedSources>true</EmbedUntrackedSources>
<GitRepositoryRemoteName>public</GitRepositoryRemoteName>
<IncludeSymbols>true</IncludeSymbols>
<SymbolPackageFormat>snupkg</SymbolPackageFormat>
</PropertyGroup>
<PropertyGroup>
<EnablePackageValidation>true</EnablePackageValidation>
<PackageValidationBaselineVersion>2.0.0</PackageValidationBaselineVersion>
<NoWarn Condition="'$(SignAssembly)' != 'true'">$(NoWarn);CP0003</NoWarn>
<NoWarn>$(NoWarn);CP0002;CP0005;CP0006</NoWarn>
<RunAnalyzersDuringBuild>False</RunAnalyzersDuringBuild>
</PropertyGroup>
<ItemGroup>
<PackageReference Include="Microsoft.NETFramework.ReferenceAssemblies" Version="1.0.3">
<PrivateAssets>all</PrivateAssets>
<IncludeAssets>runtime; build; native; contentfiles; analyzers; buildtransitive</IncludeAssets>
</PackageReference>
<PackageReference Include="Microsoft.SourceLink.GitHub" Version="8.0.0">
<PrivateAssets>all</PrivateAssets>
<IncludeAssets>runtime; build; native; contentfiles; analyzers; buildtransitive</IncludeAssets>
</PackageReference>
<PackageReference Include="Nerdbank.GitVersioning" Version="3.6.133">
<PrivateAssets>all</PrivateAssets>
<IncludeAssets>runtime; build; native; contentfiles; analyzers; buildtransitive</IncludeAssets>
</PackageReference>
</ItemGroup>
</Project>
Now let's compile:
PS C:\Users\user\bouncycastle\bc-csharp\crypto\src> dotnet publish -c Release --self-contained -r win-x64 -f net8.0
...
BouncyCastle.Crypto -> C:\Users\user\bouncycastle\bc-csharp\crypto\src\bin\Release\net8.0\win-x64\BouncyCastle.Cryptography.dll
Generating native code
Creating library bin\Release\net8.0\win-x64\native\BouncyCastle.Cryptography.lib and object
bin\Release\net8.0\win-x64\native\BouncyCastle.Cryptography.exp
BouncyCastle.Crypto -> C:\Users\user\bouncycastle\bc-csharp\crypto\src\bin\Release\net8.0\win-x64\publish\
If everything goes well, the compiled binary should be in the path bc-csharp\crypto\src\bin\Release\net8.0\win-x64\publish\native\ along with the PDB file:
Next, let's load it in IDA:
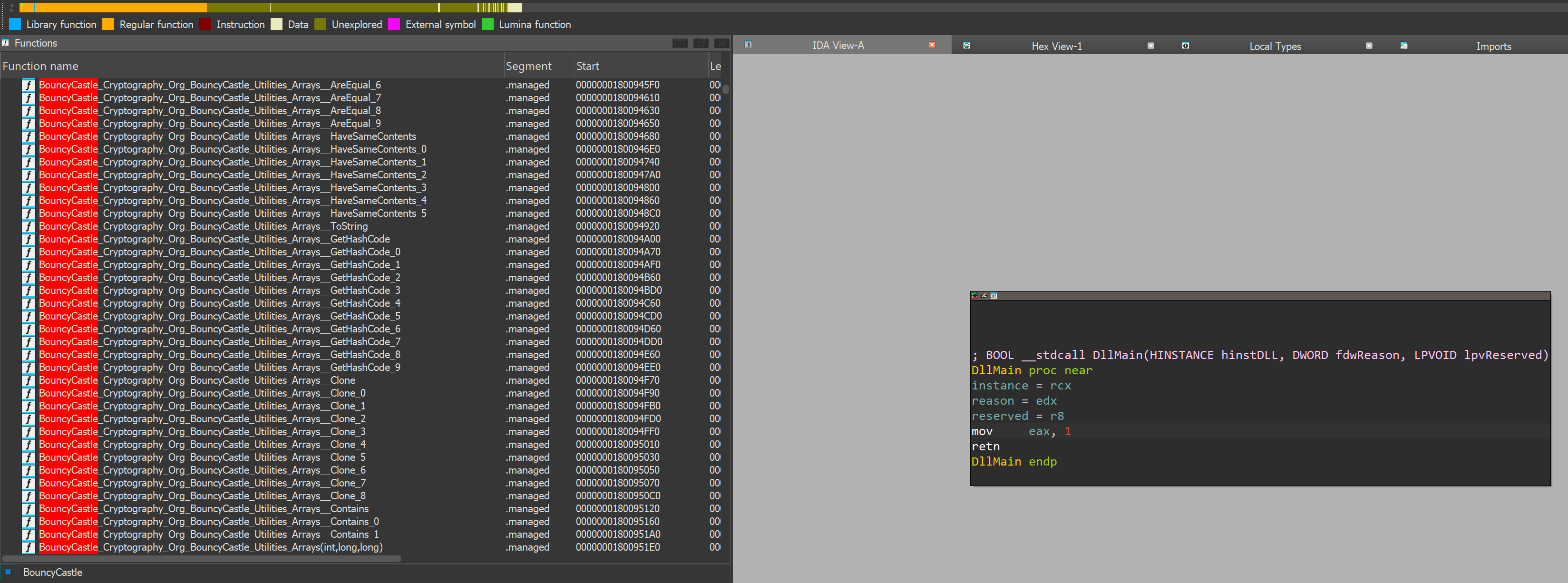
As shown, because we built the library with debug symbols, we can see all of BouncyCastle functions. The next step is to create a signature file. This can be done through IDA Pro via File -> Produce file -> Create SIG file ...
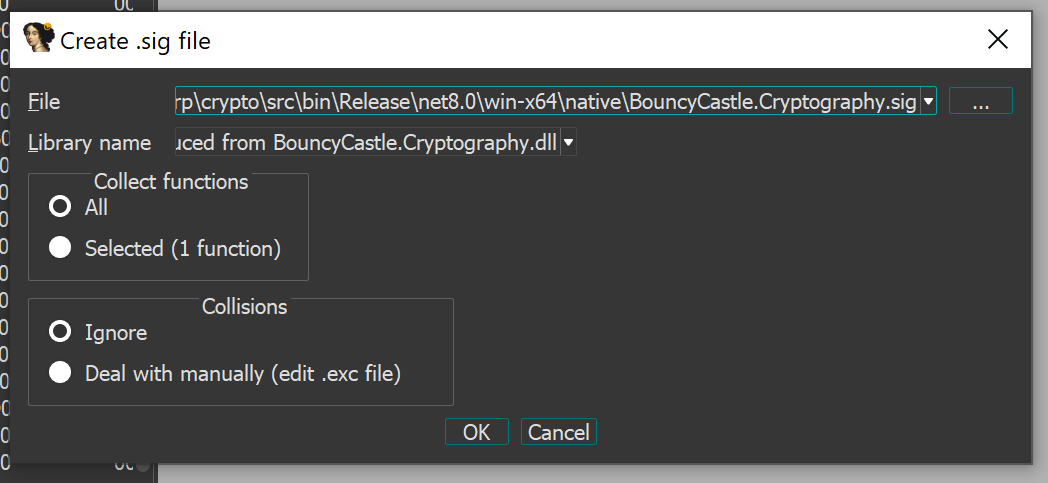
Unfortunately, this functionality seems to have a bug specifically in this scenario. When I click on OK, the program exits and produces a pattern file (.pat).

A pattern file contains byte patterns of known functions, which can be compiled separately into a FLIRT signature file using IDA's sigmake tool. Attempting to run sigmake against the produced file gives the following error:
PS C:\Users\user\bouncycastle\bc-csharp\crypto\src\bin\Release\net8.0\win-x64\native> sigmake.exe .\BouncyCastle.Cryptography.pat BouncyCastle.Cryptography.sig
.\BouncyCastle.Cryptography.pat (7586): FATAL: Bad xdigit:
This is a known issue that has already been patched in flare-ida.
Looking at the produced pattern file, I noticed the following in line 7586:

Prepending 000 to the highlighted output 17ACF fixed the issue:
PS C:\Users\user\bouncycastle\bc-csharp\crypto\src\bin\Release\net8.0\win-x64\native> sigmake.exe .\BouncyCastle.Cryptography.pat BouncyCastle.Cryptography.sig
BouncyCastle.Cryptography.sig: modules/leaves: 17172/32137, COLLISIONS: 1228
See the documentation to learn how to resolve collisions.
Now the output indicates that there are collisions. Let's ignore them by removing the first 5 lines (comments) from the produced BouncyCastle.Cryptography.exc. Once we do that, we'll be able to generate the .sig file we have been working so hard on :)
Running sigmake.exe again produces no errors:
PS C:\Users\user\bouncycastle\bc-csharp\crypto\src\bin\Release\net8.0\win-x64\native> sigmake.exe .\BouncyCastle.Cryptography.pat BouncyCastle.Cryptography.sig
Now we have a .sig file that we can load to the challenge file:

Now we'll do the same thing for the tests included in BouncyCastle project. We'll set the .csproj in bouncycastle\bc-csharp\crypto\test\BouncyCastle.Crypto.Tests.csproj to:
<Project Sdk="Microsoft.NET.Sdk">
<PropertyGroup>
<TargetFrameworks>net8.0</TargetFrameworks>
<OutputType>Exe</OutputType>
<PublishAot>true</PublishAot>
<IsPackable>false</IsPackable>
<SignAssembly>false</SignAssembly>
<EnableDefaultItems>false</EnableDefaultItems>
<NoWarn>618;1591</NoWarn>
<RootNamespace>Org.BouncyCastle</RootNamespace>
<RunAnalyzersDuringBuild>False</RunAnalyzersDuringBuild>
<Configurations>Debug;Release;Publish</Configurations>
</PropertyGroup>
<ItemGroup>
<TrimmerRootAssembly Include="BouncyCastle.Cryptography" />
</ItemGroup>
<ItemGroup>
<Compile Include="src\**\*.cs" Exclude="**\examples\**\*.cs" />
<EmbeddedResource Include="data\**\*.*" Exclude="**\README.txt" />
</ItemGroup>
<ItemGroup>
<PackageReference Include="Microsoft.NET.Test.Sdk" Version="17.10.0" />
<PackageReference Include="Microsoft.NETFramework.ReferenceAssemblies" Version="1.0.3">
<PrivateAssets>all</PrivateAssets>
<IncludeAssets>runtime; build; native; contentfiles; analyzers; buildtransitive</IncludeAssets>
</PackageReference>
<PackageReference Include="NUnit" Version="3.14.0" />
<PackageReference Include="NUnit3TestAdapter" Version="4.5.0" />
<PackageReference Include="BouncyCastle.Cryptography" Version="2.4.0" />
<PackageReference Include="Microsoft.DotNet.ILCompiler" Version="8.0.5" />
</ItemGroup>
</Project>
Then compile:
PS C:\Users\user\bouncycastle\bc-csharp\crypto\test> dotnet publish -c Release --self-contained -r win-x64 -f net8.0
This will produce a huge executable:

We'll follow the same way discussed before to produce another signature file for this executable.
After loading the two produced FLIRT signature files in IDA through File -> Load file -> FLIRT signature file..., IDA successfully finds many BouncyCastle functions:
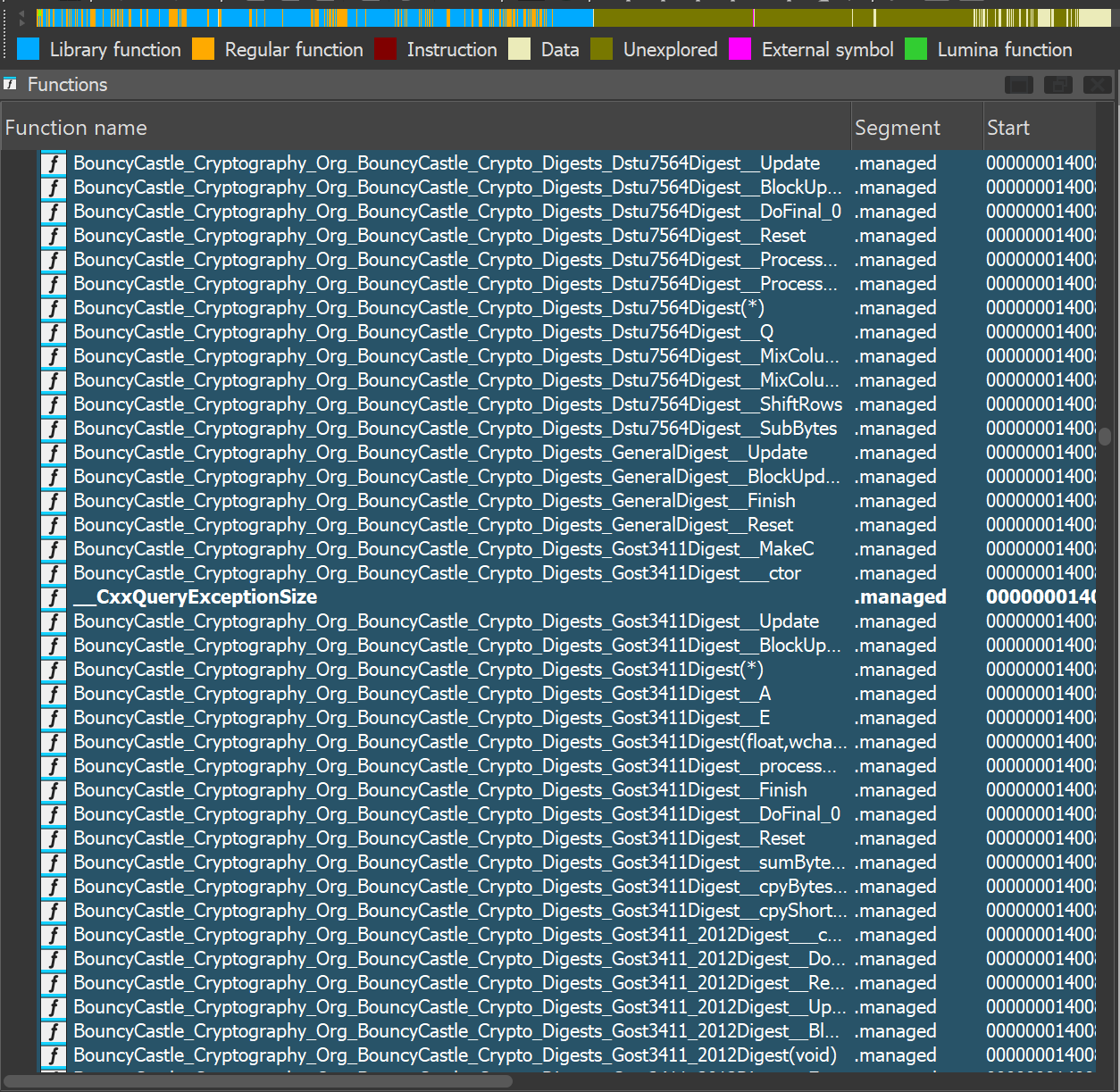
Great. We should keep in mind that IDA might have missed some functions, so we might be required to produce more signature files later on.
Next, we need to know the starting point of the program. In other words, executable .NET programs usually have a function that they start from. We need to identify where this is.
For this, let's write a hello world program that just sends and receives some data:
using System;
using System.Net;
using System.Net.Sockets;
using System.Text;
class Program
{
static void Main()
{
string serverIp = "127.0.0.1";
int port = 31337;
byte[] sendBuffer = Encoding.UTF8.GetBytes("Hello, server!");
try
{
// Create a TCP client and connect to the server
using (TcpClient client = new TcpClient())
{
client.Connect(IPAddress.Parse(serverIp), port);
Console.WriteLine("Connected to server.");
// Get the network stream to send and receive data
using (NetworkStream stream = client.GetStream())
{
// Send data to the server
Console.WriteLine("Sending data to server...");
stream.Write(sendBuffer, 0, sendBuffer.Length);
// Receive data from the server
byte[] receiveBuffer = new byte[1024]; // Buffer to hold the response
int bytesRead = stream.Read(receiveBuffer, 0, receiveBuffer.Length);
// Display the received data
string receivedData = Encoding.UTF8.GetString(receiveBuffer, 0, bytesRead);
Console.WriteLine("Received from server: " + receivedData);
}
}
}
catch (Exception ex)
{
Console.WriteLine("Error: " + ex.Message);
}
}
}
We'll create a new project and put the following XML in its .csproj file:
<Project Sdk="Microsoft.NET.Sdk">
<PropertyGroup>
<OutputType>Exe</OutputType>
<TargetFramework>net8.0</TargetFramework>
<PublishAot>true</PublishAot>
<ImplicitUsings>enable</ImplicitUsings>
<Nullable>enable</Nullable>
</PropertyGroup>
<ItemGroup>
<PackageReference Include="BouncyCastle.Cryptography" Version="2.4.0" />
<PackageReference Include="Microsoft.DotNet.ILCompiler" Version="8.0.5" />
</ItemGroup>
</Project>
Once it's compiled, we'll load it in IDA and search for its main function:
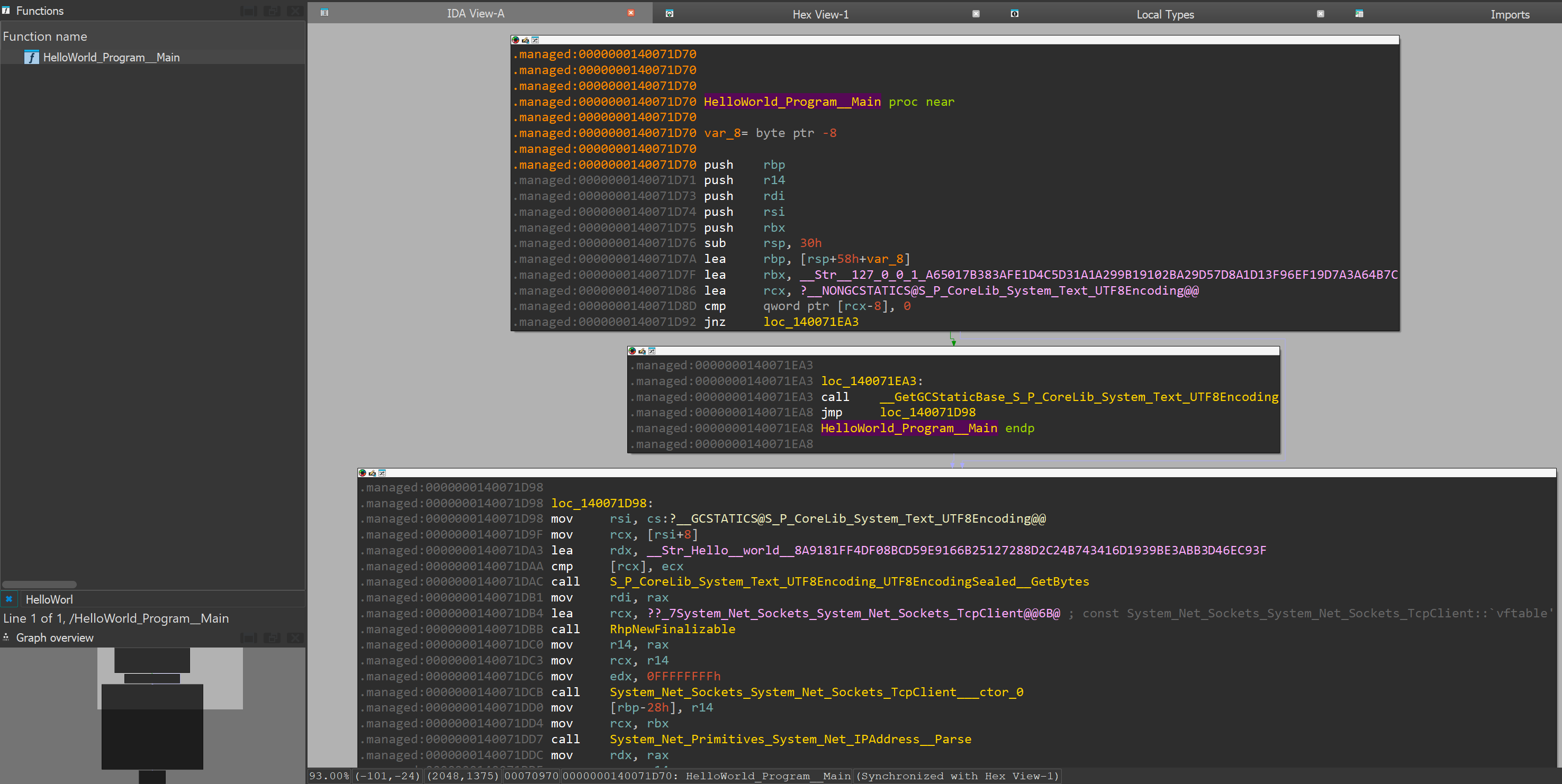
As shown, this is the main function of our .net program. This function is called from __managed__Main:
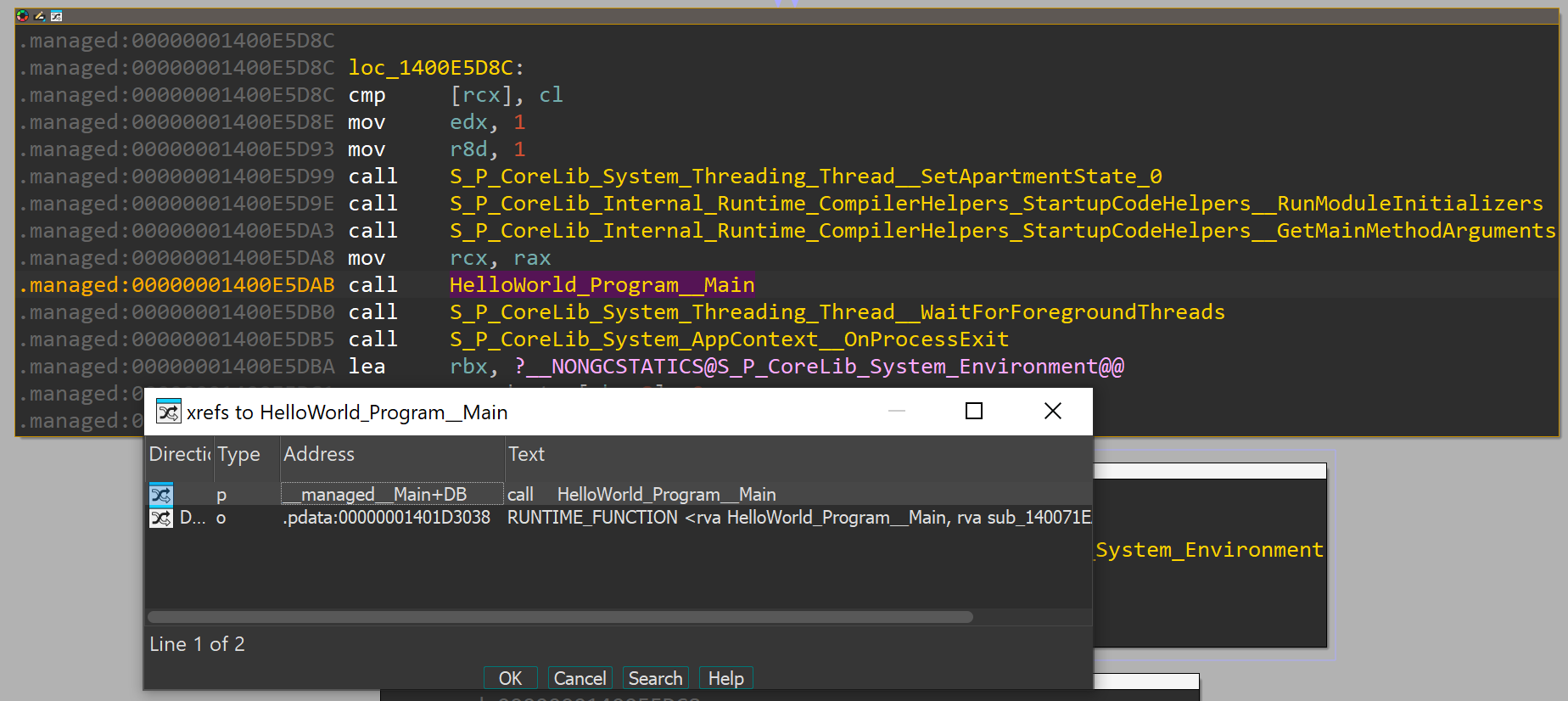
Let's compare the two programs' __managed_Main side by side:

The figure shows that the function sub_140108AC0 is most likely the program main of the challenge program, so we can start our analysis from there. We can also create a signature file for our Hello World program and import it into our challenge file, which might help identify any TCP/IP communication functions.
The first function call we encounter in the program main of the target binary is a call to sub_140001ED4:
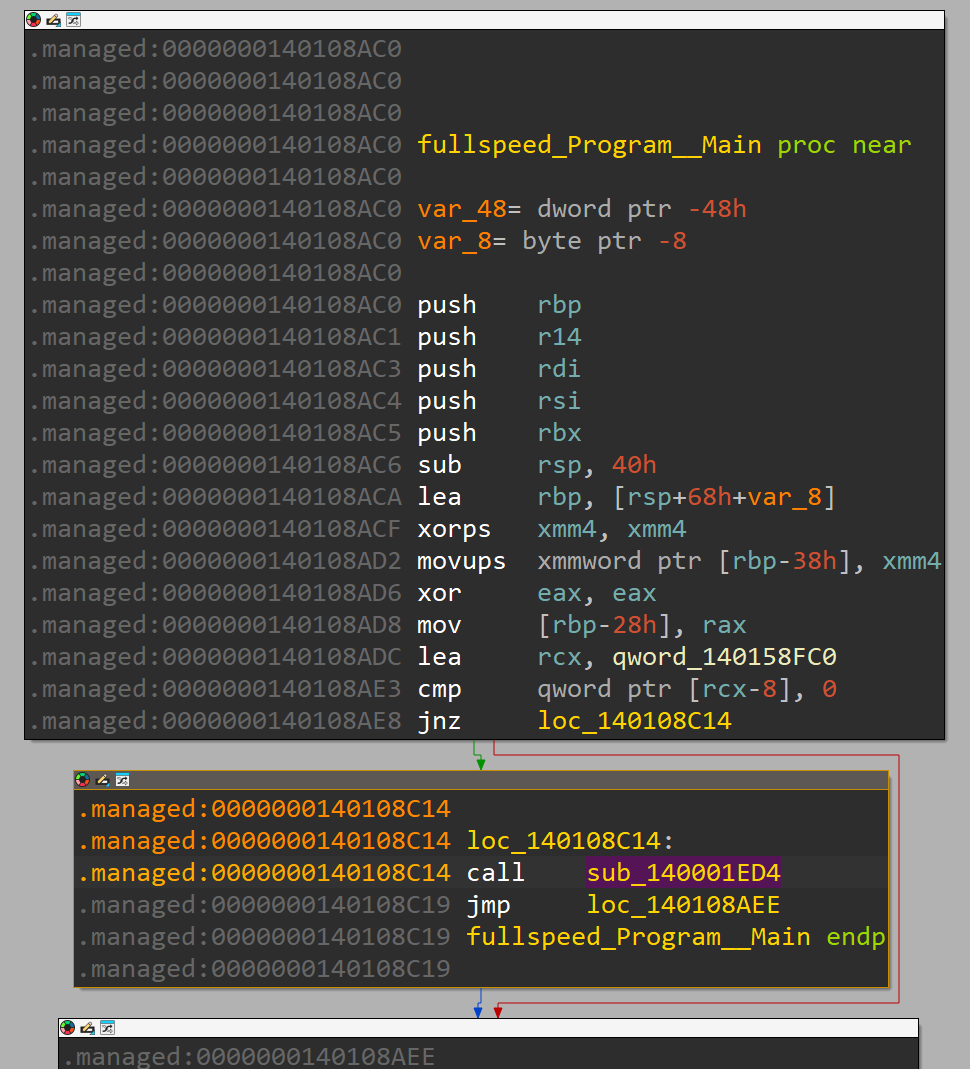
If we inspect its code, we find that this function jumps into S_P_CoreLib_System_Runtime_CompilerServices_ClassConstructorRunner__CheckStaticClassConstructionReturnGCStaticBase. From the name, we know that this must be relevant to class construction.
Upon further analysis of the internals of S_P_CoreLib_System_Runtime_CompilerServices_ClassConstructorRunner__CheckStaticClassConstructionReturnGCStaticBase, I noticed that the program calls the constructor at this location:
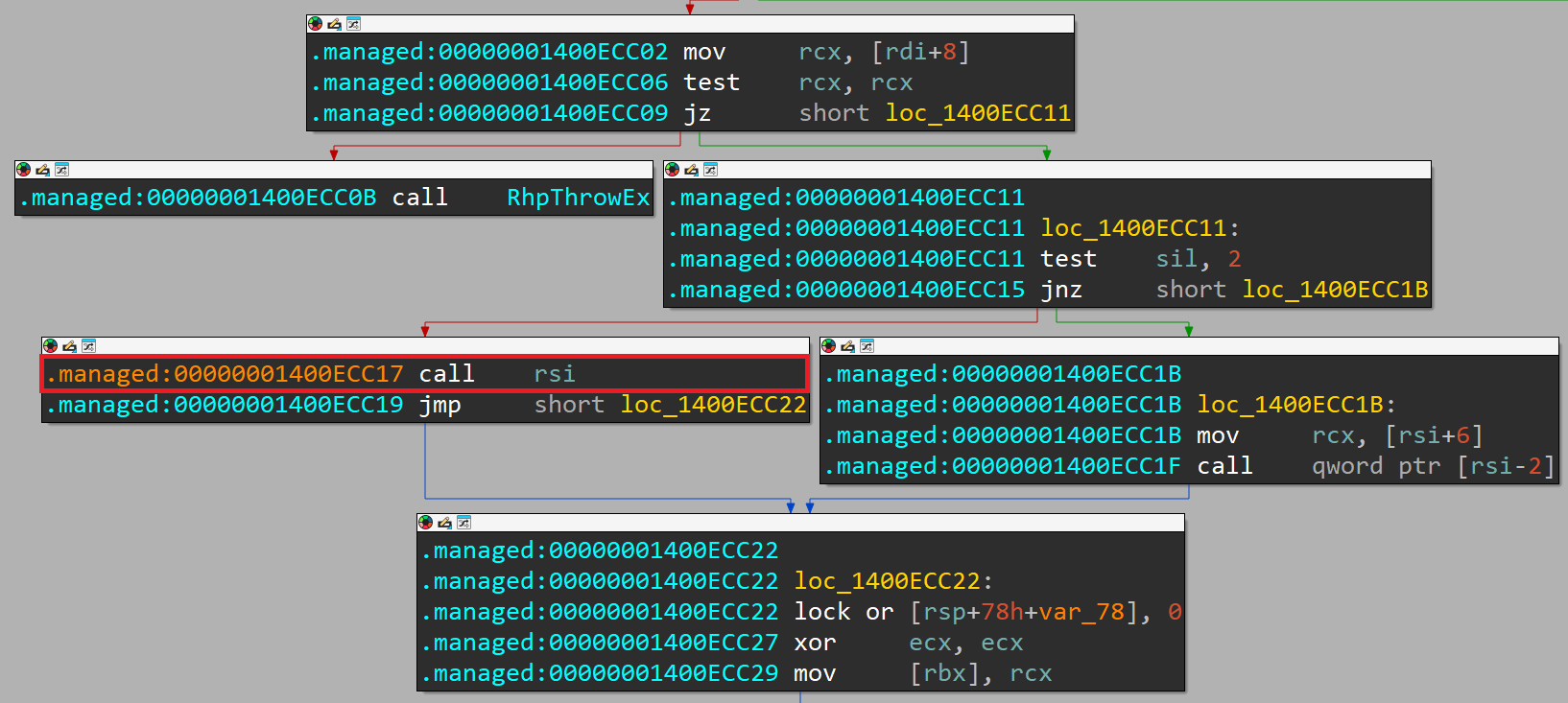
Let's set a breakpoint on the program main and another one at the place where the constructor is called (shown above) to figure out what constructor is being called at the start of the program's main:
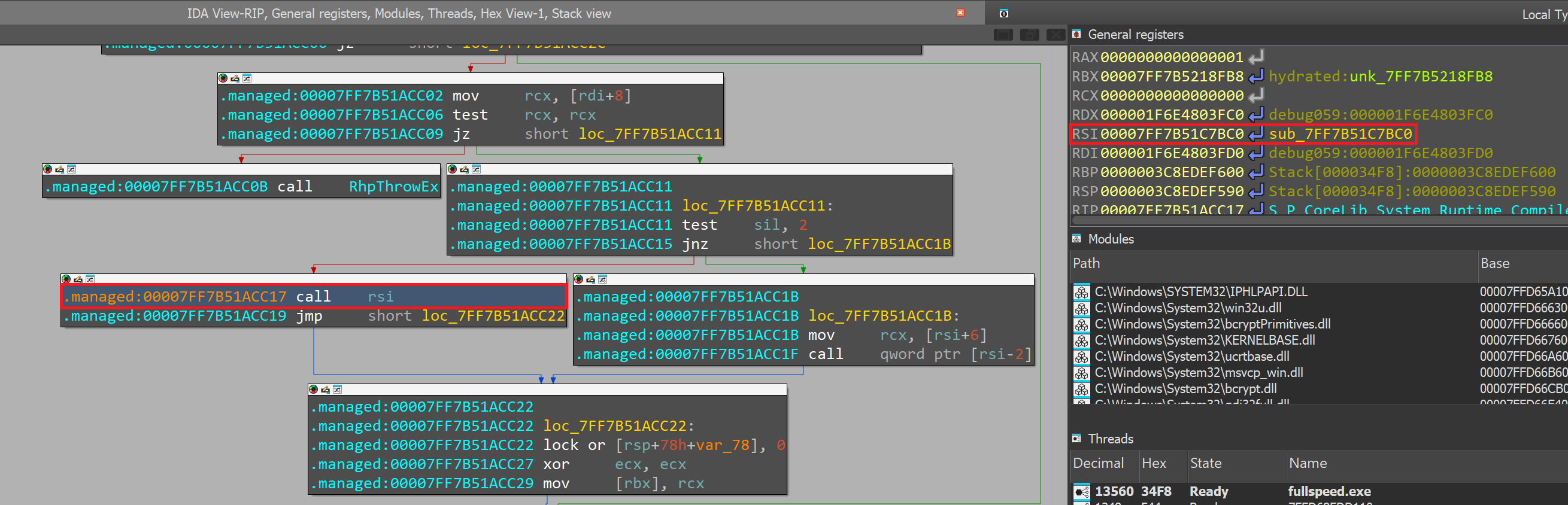
Once the execution hits the program main breakpoint, we'll let it continue until hitting the place where the constructor is called.
From here, we know that the constructor is sub_7FF7B51C7BC0 (image above). Let's rename it to fullspeed_constructor.
In this constructor, there are several calls to BouncyCastle_Cryptography_Org_BouncyCastle_Math_BigInteger___ctor_1 and another call to BouncyCastle_Cryptography_Org_BouncyCastle_Math_EC_FpCurve___ctor_1.
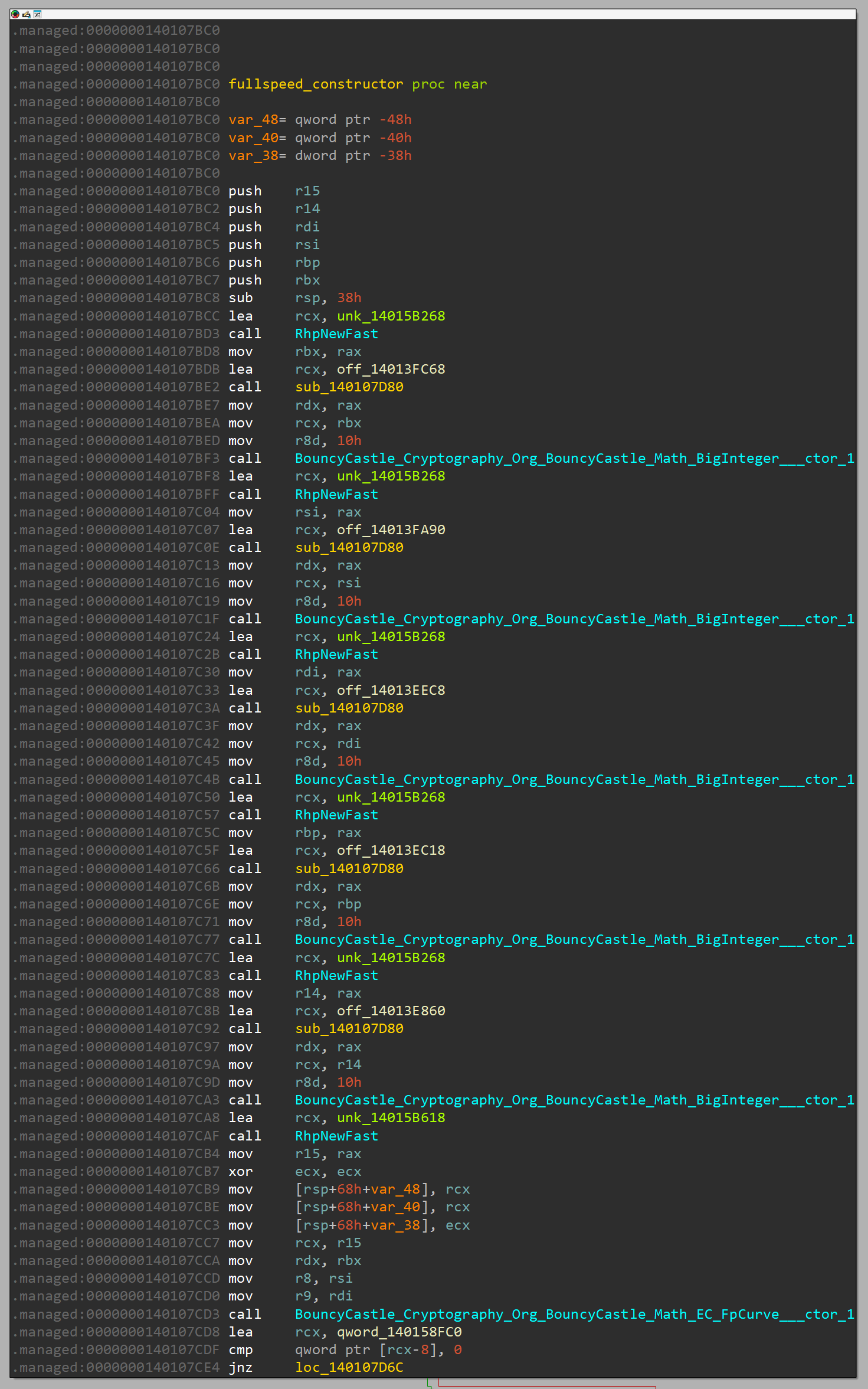
In BouncyCastle, BigInteger is used to create a BigInteger from a hexadecimal string representation, which is then utilized in cryptographic operations. FpCurve is used to define an elliptic curve for such operations.
The code shown should look similar to the following:
BigInteger p = new BigInteger("...");
BigInteger a = new BigInteger("...");
BigInteger b = new BigInteger("...");
BigInteger gx = new BigInteger("...");
BigInteger gy = new BigInteger("...");
FpCurve curve = new FpCurve(p, a, b);
The naming of the variables is based on the algorithm used and the fact that there are 5 numbers being converted to BigIntegers.
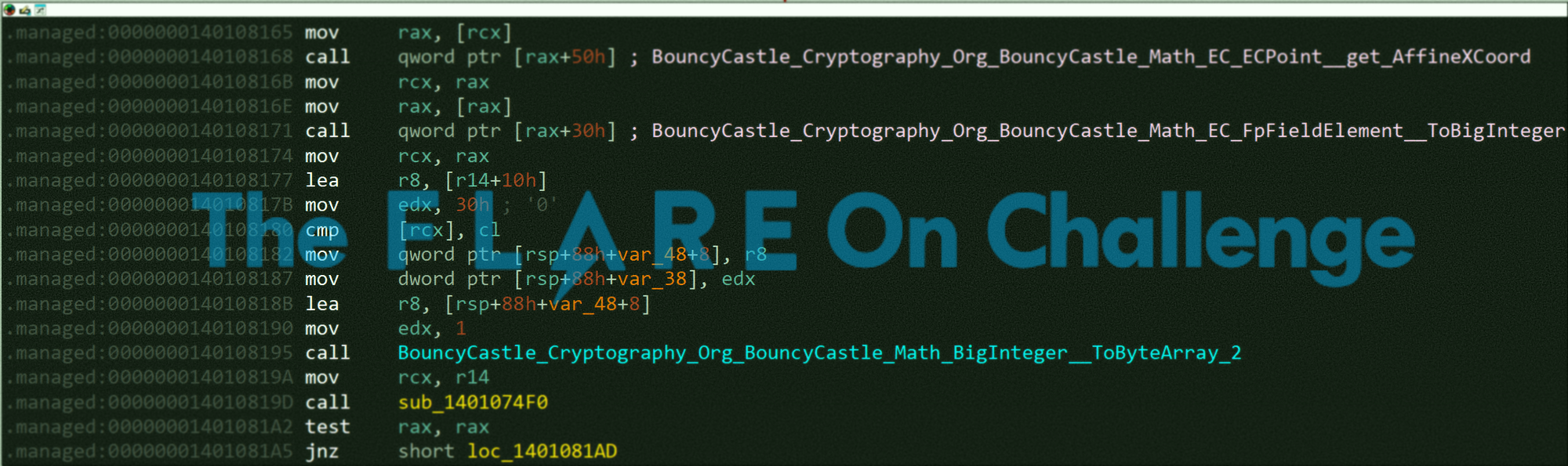
Now to obtain the exact values passed to BigInteger, we need first to understand what sub_140107D80 does as it's being called every time before BigInteger is called. The code of this function is shown in the following figure:
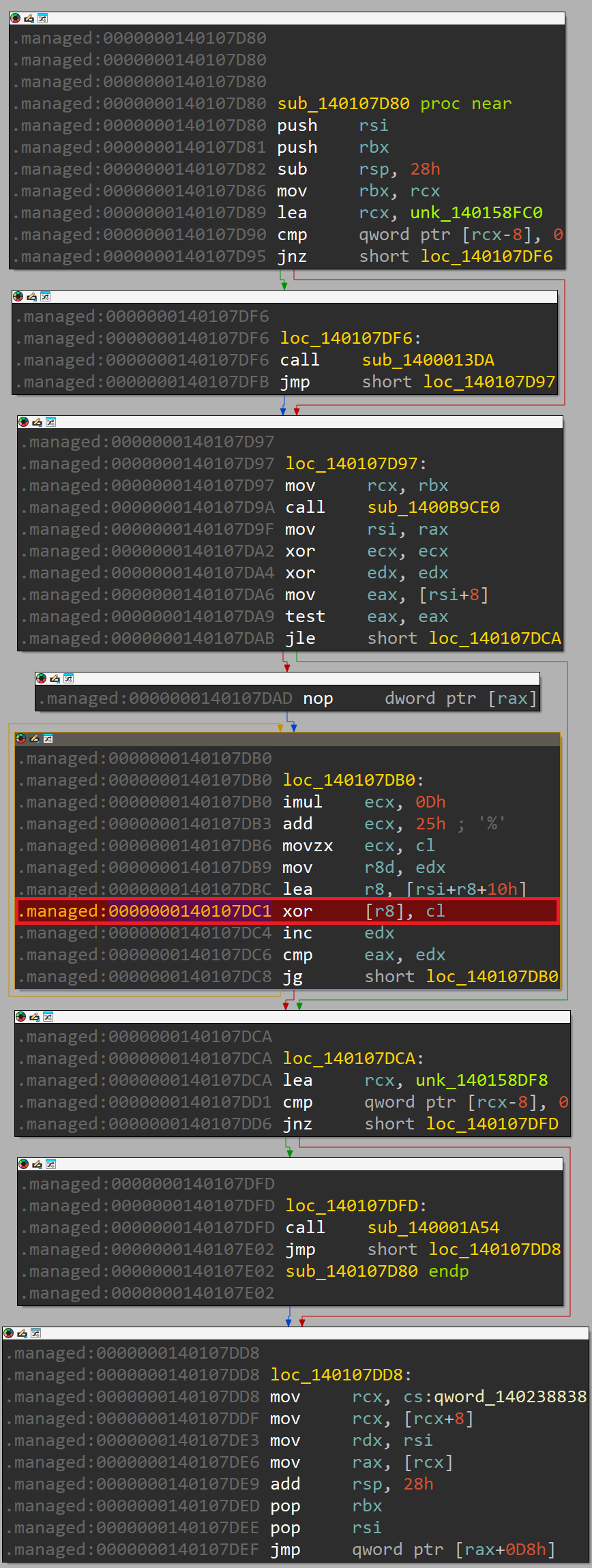
As shown, this function actually performs a simple XOR algorithm for a hard-coded data. Let's rename it to XORcrypt.
To see what it's trying to decrypt, we can set a breakpoint at 0x140107DC1 and inspect the value r8 points to:
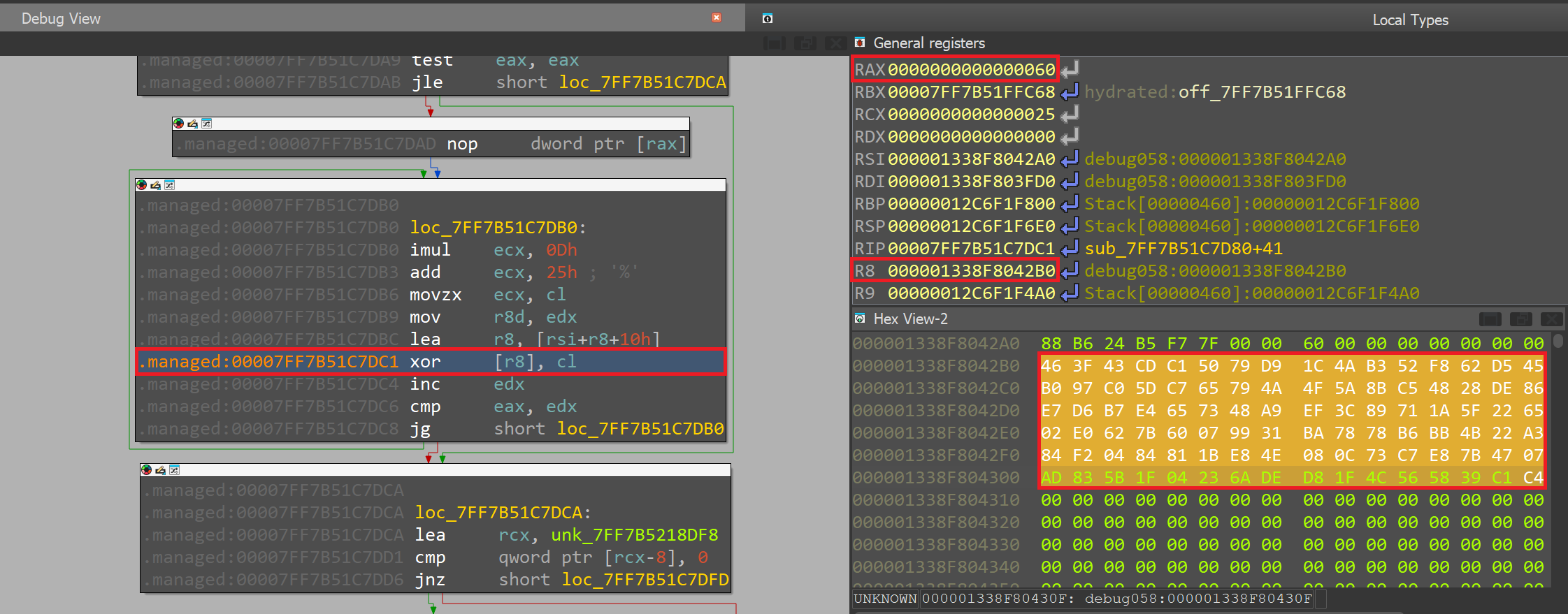
We can implement this algorithm in Python:
def crypt(b:bytes):
result = []
ecx = 0
for i in range(len(b)):
ecx *= 0xd
ecx += 0x25
cl = ecx & 0xff
result.append(b[i] ^ cl)
return bytes(result)
Passing the encrypted value to this function, we get the following:
In [2]: crypt(bytes.fromhex("463F43CDC15079D91C4AB352F862D545B097C05DC765794A4F5A8BC54828DE86E7D6B7E4657348A9EF3C89711A5F226502E0627B60079931BA7878B6BB4B22A384F20484811BE84E080C73C7E87B4707AD835B1F04236ADED81F4C565839C1C4"))
Out[2]: b'c90102faa48f18b5eac1f76bb40a1b9fb0d841712bbe3e5576a7a56976c2baeca47809765283aa078583e1e65172a3fd'
This means that the first decrypted value is c90102faa48f18b5eac1f76bb40a1b9fb0d841712bbe3e5576a7a56976c2baeca47809765283aa078583e1e65172a3fd, which corresponds to the prime value p. We can confirm this:
In [3]: import sympy
In [4]: sympy.isprime(0xc90102faa48f18b5eac1f76bb40a1b9fb0d841712bbe3e5576a7a56976c2baeca47809765283aa078583e1e65172a3fd)
Out[4]: True
We can do the same for the other values to decrypt them. Once we do that, we'll get the following values:
// prime modulus
BigInteger p = new BigInteger("c90102faa48f18b5eac1f76bb40a1b9fb0d841712bbe3e5576a7a56976c2baeca47809765283aa078583e1e65172a3fd");
// Curve coefficient
BigInteger a = new BigInteger("a079db08ea2470350c182487b50f7707dd46a58a1d160ff79297dcc9bfad6cfc96a81c4a97564118a40331fe0fc1327f");
// Curve coefficient
BigInteger b = new BigInteger("9f939c02a7bd7fc263a4cce416f4c575f28d0c1315c4f0c282fca6709a5f9f7f9c251c9eede9eb1baa31602167fa5380");
// Generator point x-coordinate
BigInteger gx = new BigInteger("087b5fe3ae6dcfb0e074b40f6208c8f6de4f4f0679d6933796d3b9bd659704fb85452f041fff14cf0e9aa7e45544f9d8");
// Generator point y-coordinate
BigInteger gy = new BigInteger("127425c1d330ed537663e87459eaa1b1b53edfe305f6a79b184b3180033aab190eb9aa003e02e9dbf6d593c5e3b08182");
The next part of the constructor performs an indirect call:
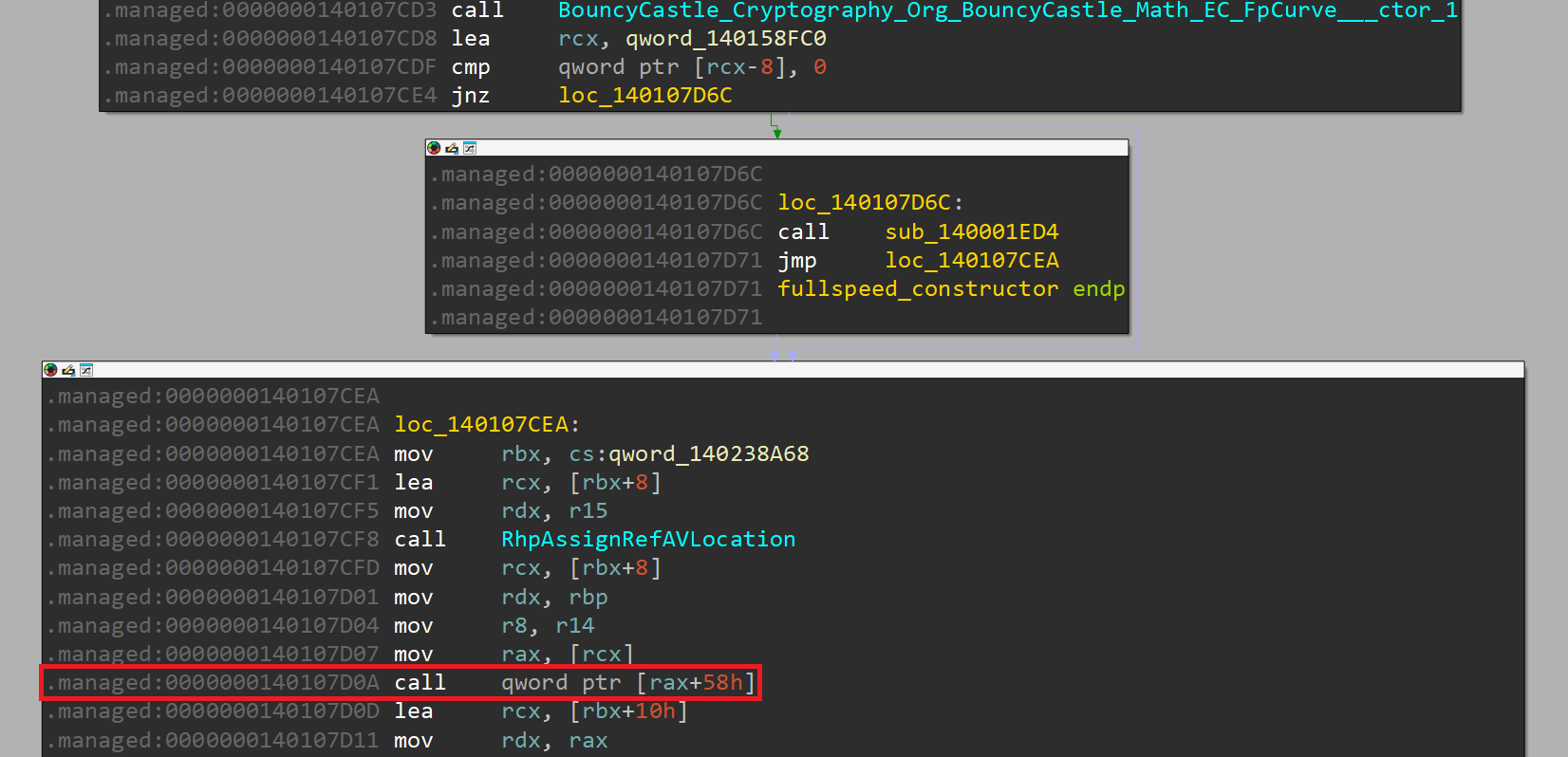
Let's set a break point and inspect the function being called:
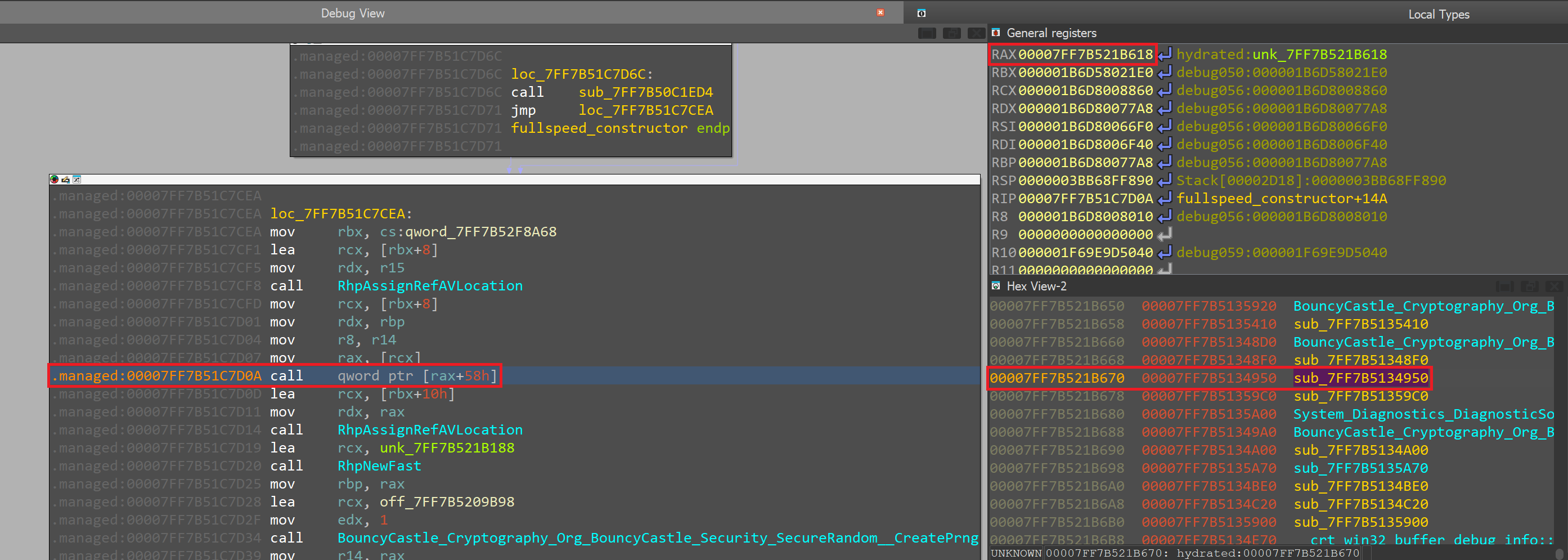
Unfortunately, we haven't identified this function. If we inspect this function, we'll notice that there are two indirect calls and an indirect jump. If we inspect those as well, we'll notice that they point to other functions within BouncyCastle. This means that this function is most likely a function in BouncyCastle library.
After spending sometime analyzing BouncyCastle, I noticed that this function is very similar to BouncyCastle_Cryptography_Org_BouncyCastle_Math_EC_ECCurve__CreatePoint in the library we have compiled earlier:
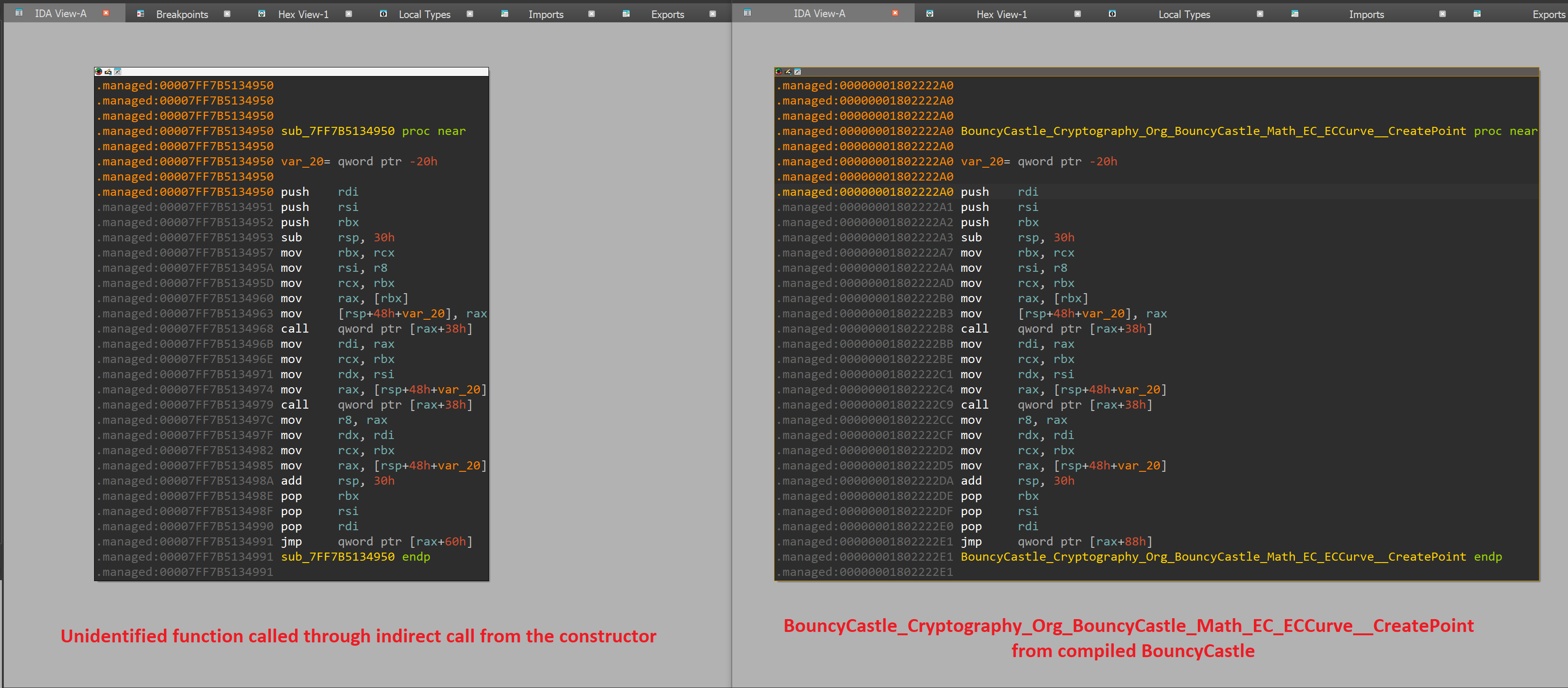
With this in mind, we'll change the name of the unidentified function to BouncyCastle_Cryptography_Org_BouncyCastle_Math_EC_ECCurve__CreatePoint, and we'll leave a comment where it's called highlighting that it will be called there:
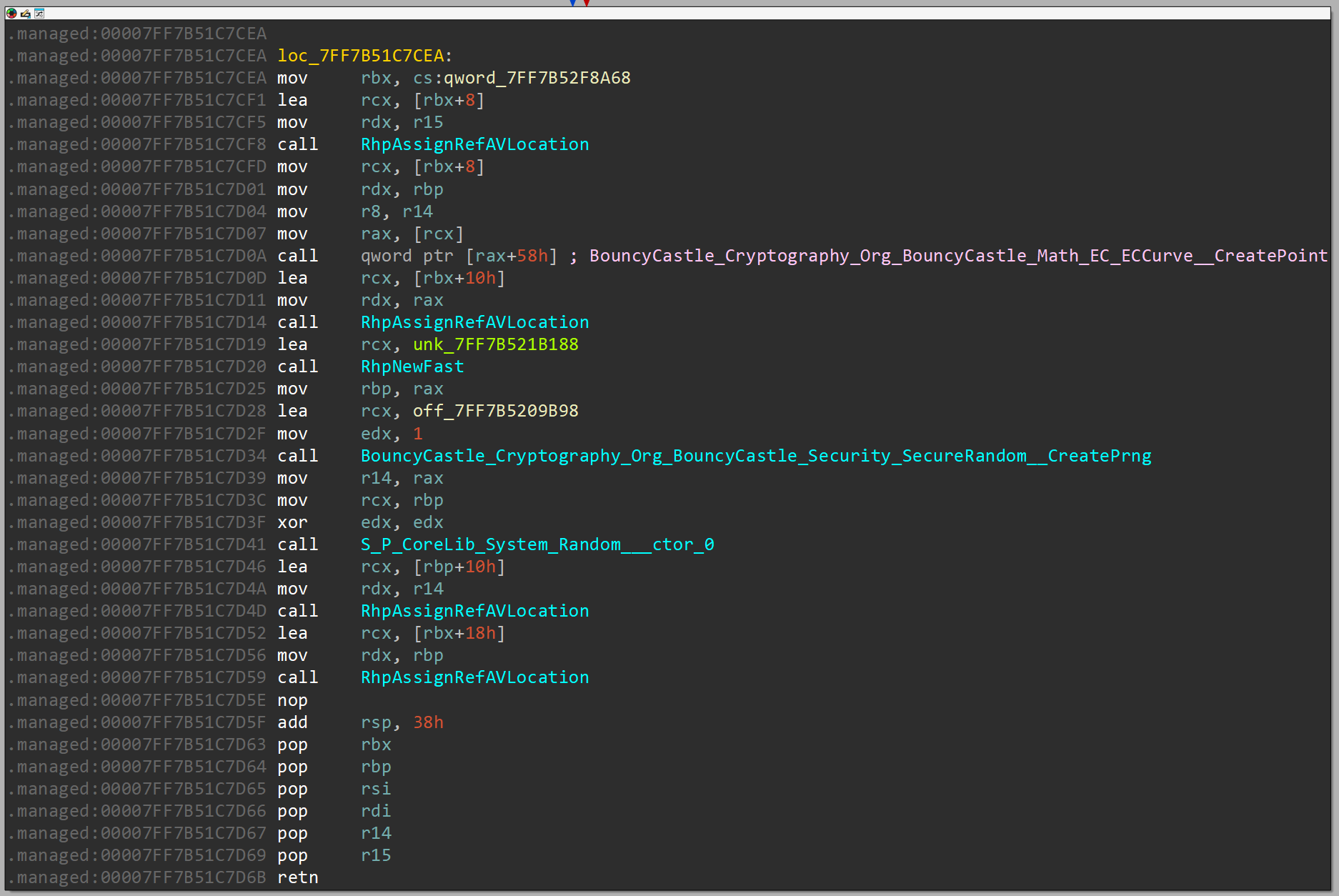
After creating the curve, the program creates a generator point G using the values of gx and gy. This point is essential for cryptographic operations such as generating the public key, ...etc. The constructor does something similar to this:
BigInteger p = new BigInteger("c90102faa48f18b5eac1f76bb40a1b9fb0d841712bbe3e5576a7a56976c2baeca47809765283aa078583e1e65172a3fd");
BigInteger a = new BigInteger("a079db08ea2470350c182487b50f7707dd46a58a1d160ff79297dcc9bfad6cfc96a81c4a97564118a40331fe0fc1327f");
BigInteger b = new BigInteger("9f939c02a7bd7fc263a4cce416f4c575f28d0c1315c4f0c282fca6709a5f9f7f9c251c9eede9eb1baa31602167fa5380");
BigInteger gx = new BigInteger("087b5fe3ae6dcfb0e074b40f6208c8f6de4f4f0679d6933796d3b9bd659704fb85452f041fff14cf0e9aa7e45544f9d8");
BigInteger gy = new BigInteger("127425c1d330ed537663e87459eaa1b1b53edfe305f6a79b184b3180033aab190eb9aa003e02e9dbf6d593c5e3b08182");
FpCurve curve = new FpCurve(p, a, b);
var G = curve.CreatePoint(gx, gy);
At the end of the constructor, it calls BouncyCastle_Cryptography_Org_BouncyCastle_Security_SecureRandom__CreatePrng and S_P_CoreLib_System_Random___ctor_0 to create a Pseudo-Random Number Generator (PRNG), which might be used later for creating a private key.
Now that we have covered the program constructor, let's go back to the program main. Right after the function sub_140001ED4 that calls the constructor, we notice the following block:
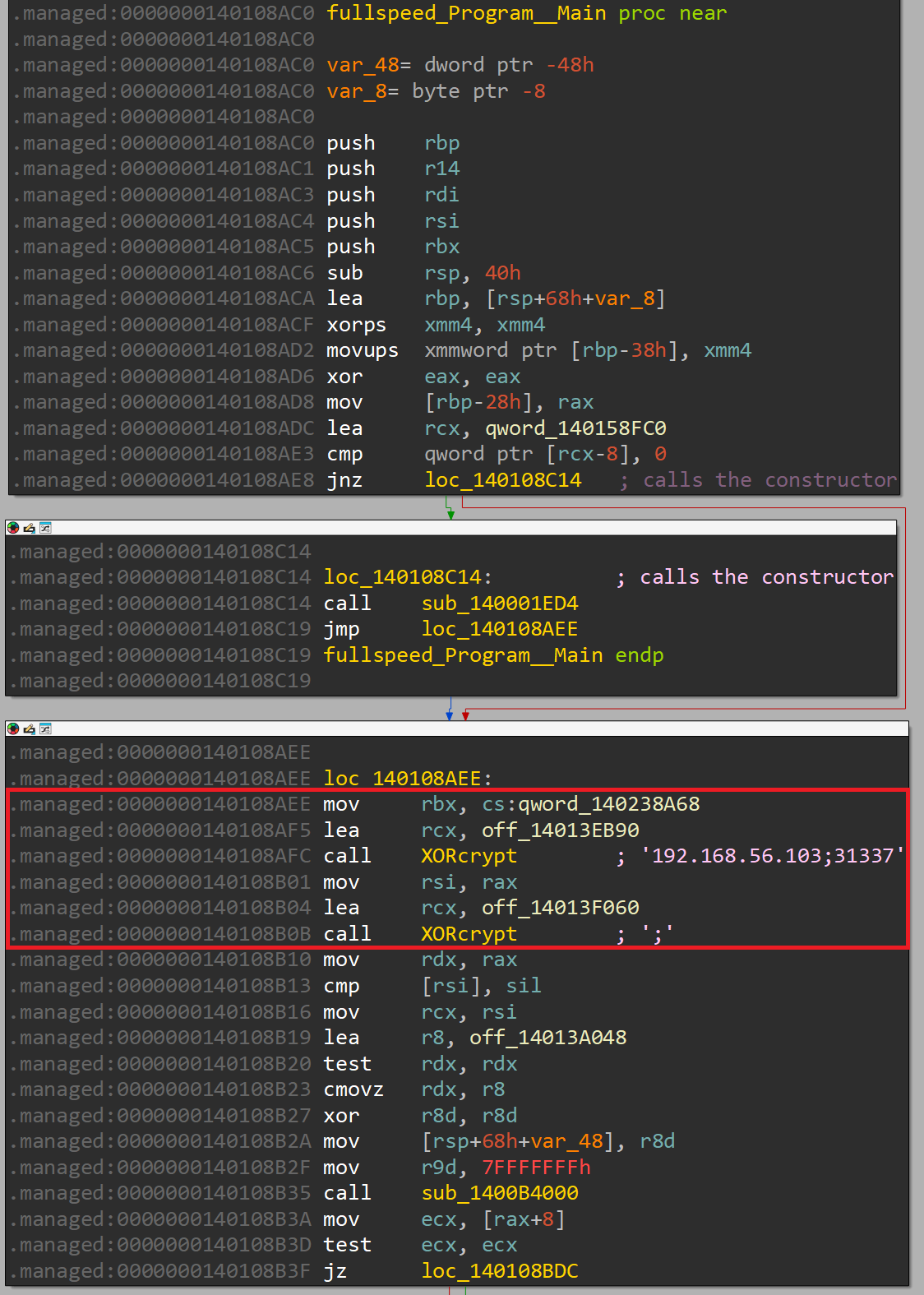
As shown, if we follow the same method discussed earlier to decrypt data, we'll see that the the program attempts to decrypt the IP address and port to be used for communication.
Next, we notice two interesting function calls in the following block in program main:
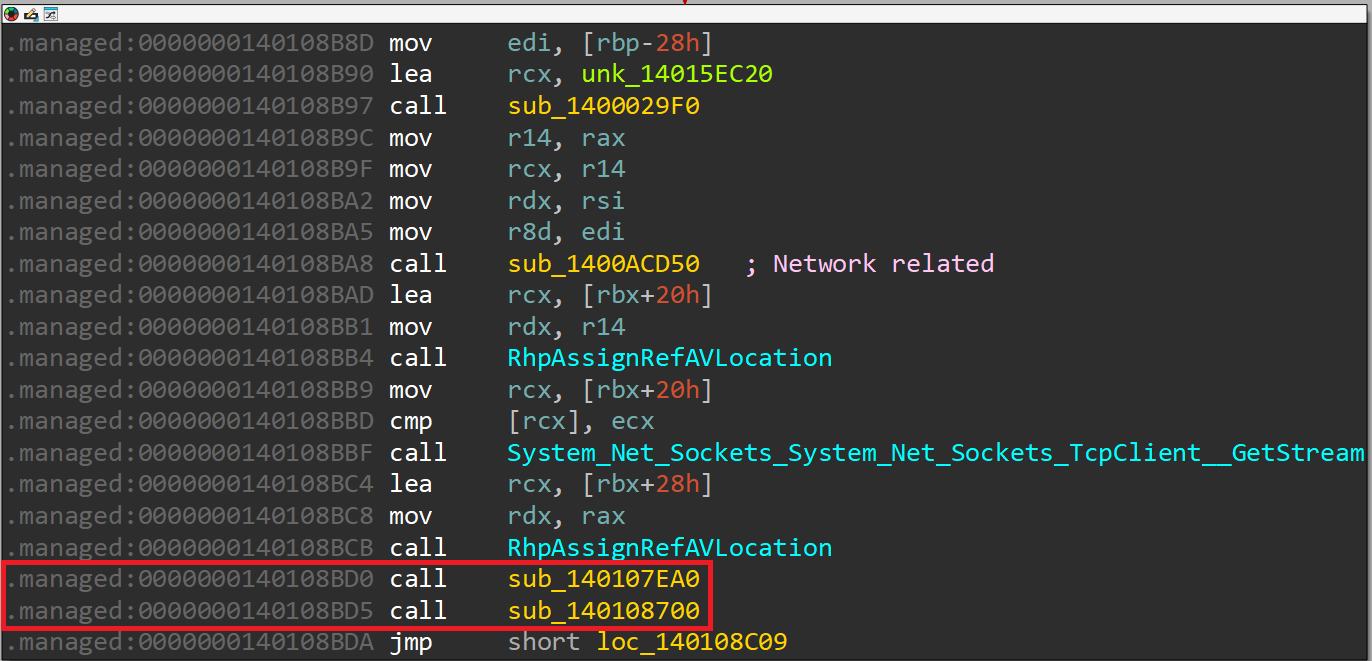
It turns out that these two functions are the core of the program's logic.
A quick analysis of the first function sub_140107EA0 reveals that it's responsible for communicating with the server based on the following blocks:
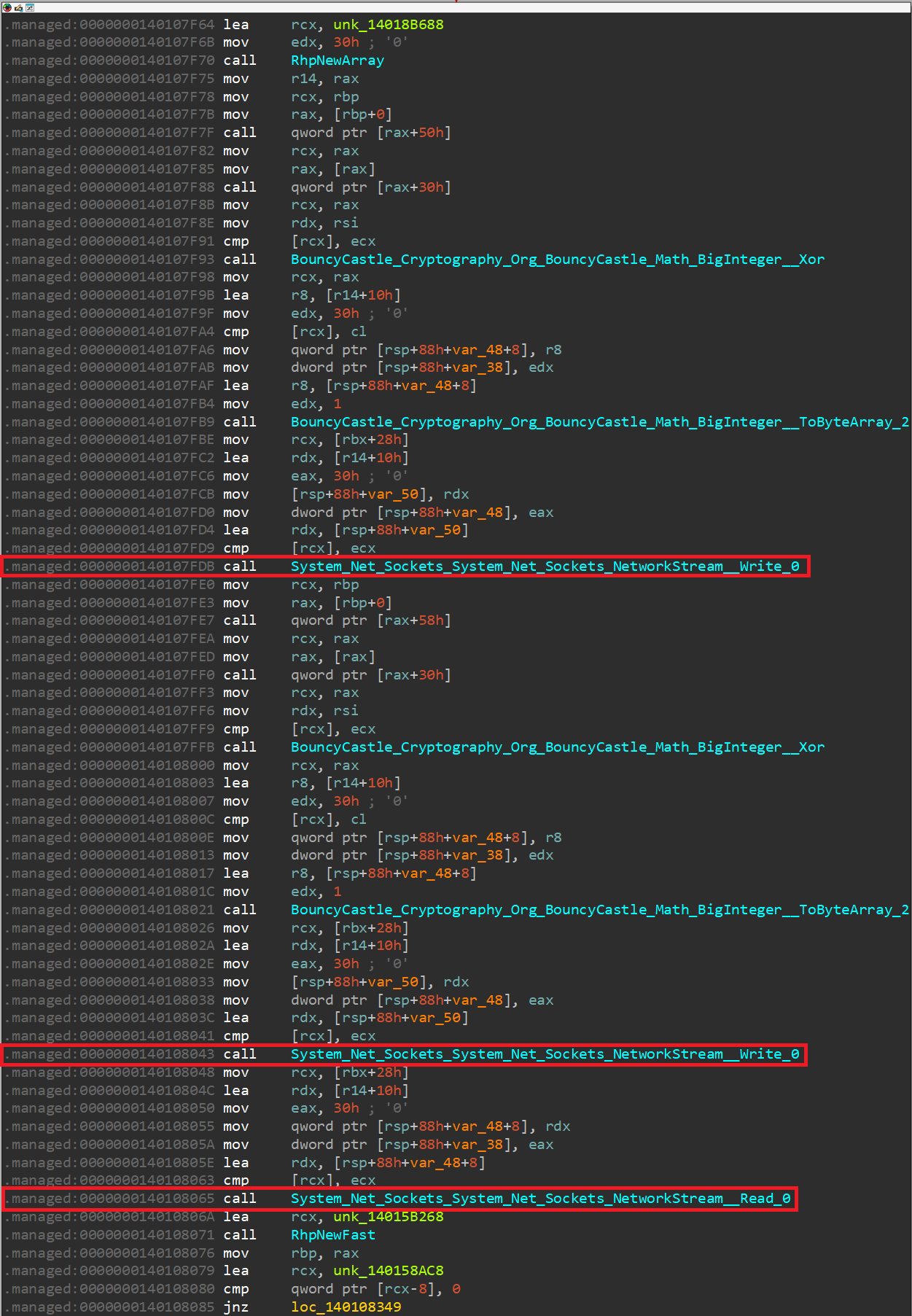
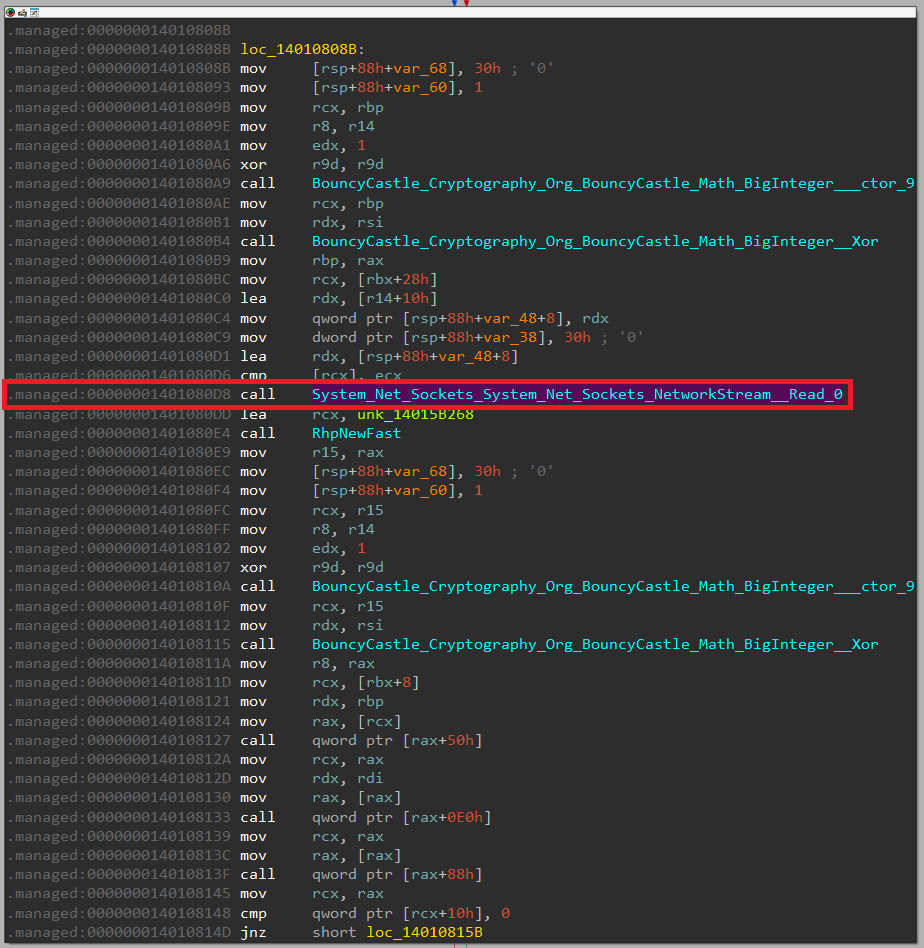
For this reason, let's rename it to server_communication.
The second function call sub_140108700 contains sequential string checks:
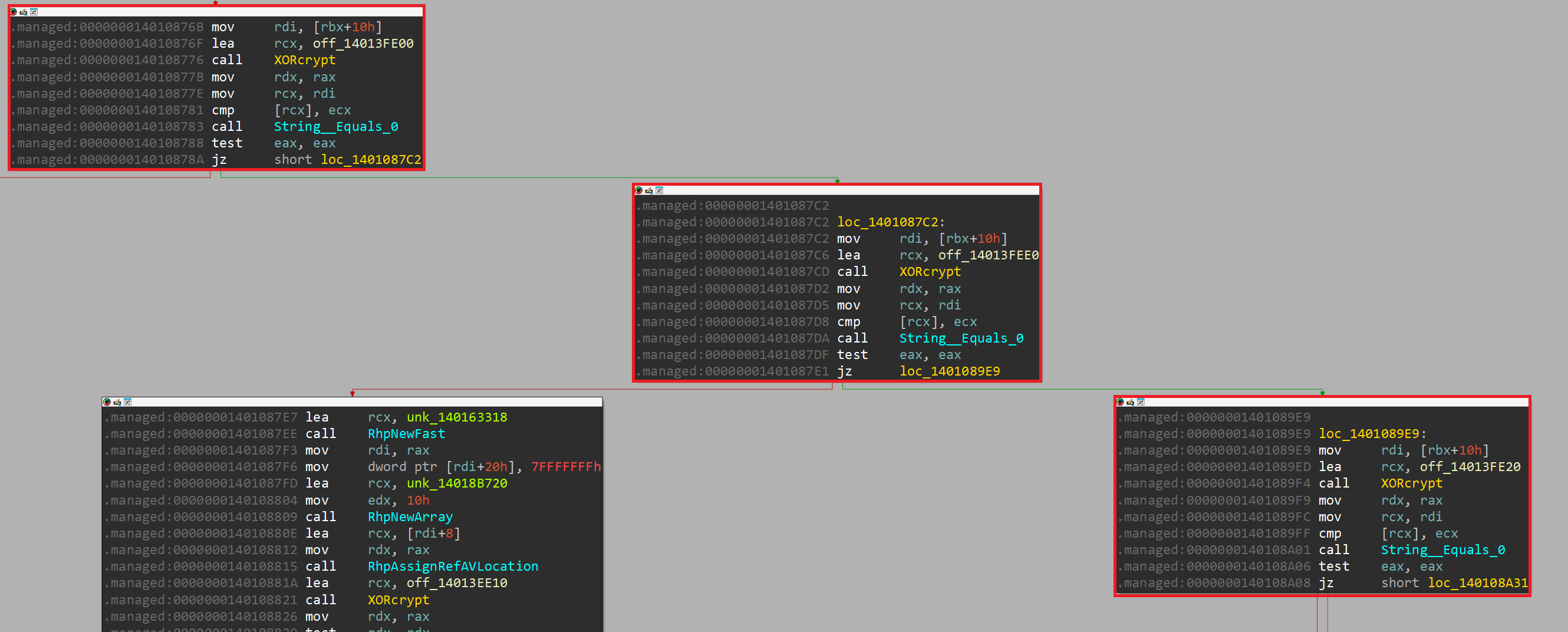
This suggests that this function is used to parse potential strings/commands received from the server. Due to this, we'll rename this function to handle_cmd.
Since we're more interested in understanding the communication, as we're given a PCAP file, let's focus more on server_communication to understand the communication logic.
Before we do so, let's write a dummy server that prints the received buffer from the client. This is required because if the client (program) is not able to connect to a server, it will eventually exit and will not reach the server_communication function.
We'll also need to keep in mind that the server's IP address 192.168.56.103 is hard-coded in the client, so we'll need to either create a separate network interface and assign this IP or just force our IP to be 192.168.56.103 in one of the existing network interfaces. I'll opt for the latter option.
The following is the dummy server:
import socket
server = socket.socket(socket.AF_INET, socket.SOCK_STREAM)
server.bind(('192.168.56.103', 31337))
server.listen(1)
print("Server listening on 192.168.56.103:31337")
while True:
try:
client, addr = server.accept()
print(f"Client connected from {addr}")
# Receive first 48 bytes
buffer1 = client.recv(48)
print(f"buffer 1: {buffer1.hex()}")
# Receive second 48 bytes
buffer2 = client.recv(48)
print(f"buffer 2: {buffer2.hex()}")
# Wait
client.recv(1)
except KeyboardInterrupt:
client.close()
Once we run the server, we'll be able to continue our analysis.
$ python server.py
Now that the server is running, we'll place a breakpoint on the first call to XORcrypt in server_communication. We notice that the program decrypts another value. The result of the decryption is 133713371337133713371337133713371337133713371337133713371337133713371337133713371337133713371337. This value is then converted to a BigInteger.
Next, we have the following block:
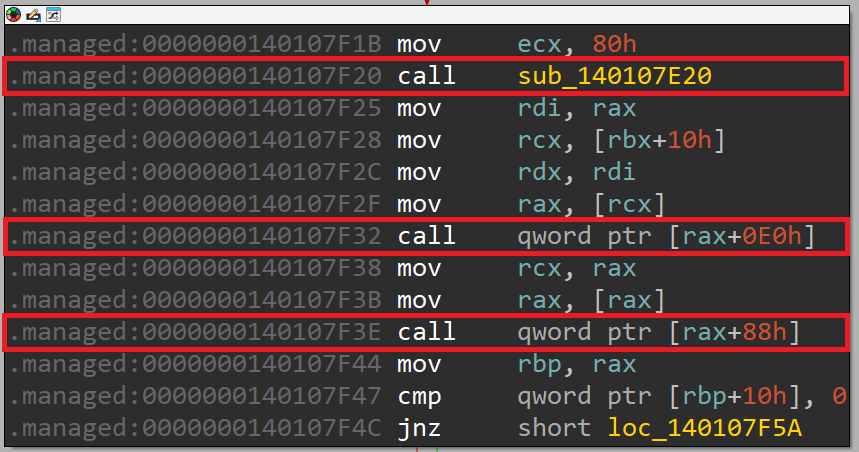
This block contains several indirect calls as well as a call to the function sub_140107E20. Let's explore this function:
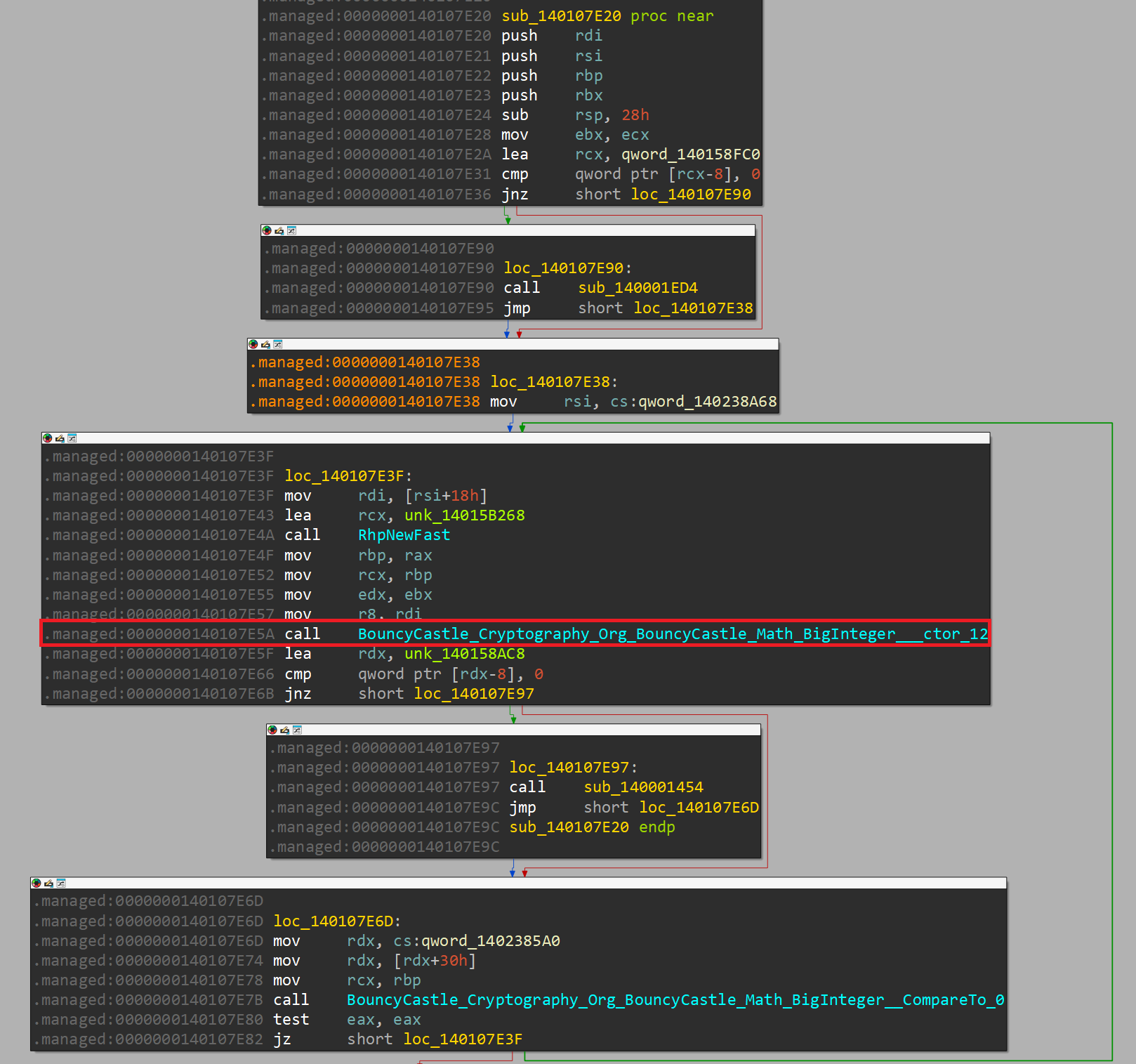
This function contains a call to the constructor BouncyCastle_Cryptography_Org_BouncyCastle_Math_BigInteger___ctor_12. If we place a breakpoint on it, we'll notice that it takes the following arguments:
- an object representing
this, which is a reference to the instance being constructed (RCX). - first constructor argument (
RDX). - second constructor argument (
R8). - third constructor argument (
R9). - The rest are pushed to the stack.
In this case, the constructor takes 2 arguments excluding the object reference. Since we're mostly interested in the actual constructor arguments, we'll inspect RDX and R8:
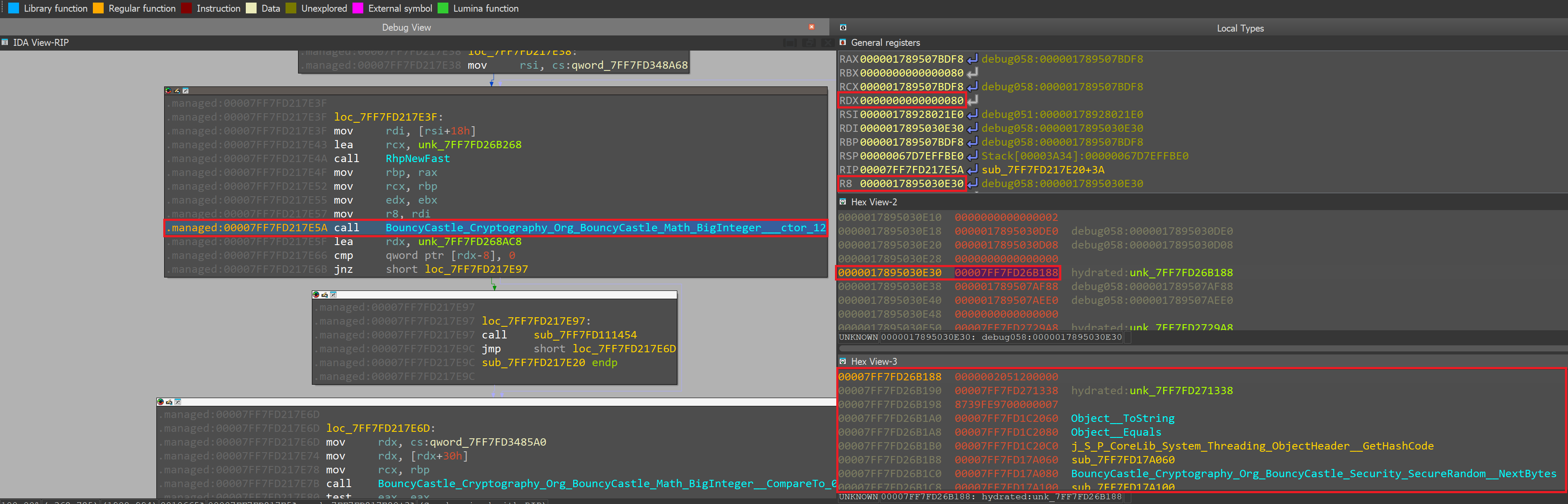
The first argument is the value 0x80 (128 in decimal). The second argument is an object representing a reference to the secure random that the program created earlier. In essence, the program is generating a 16-byte value using SecureRandom PRNG. The code in C# looks as follows:
SecureRandom random = new SecureRandom(); // done earlier
BigInteger value = new BigInteger(128, random);
We can inspect this value through stepping over and inspecting RDX value:
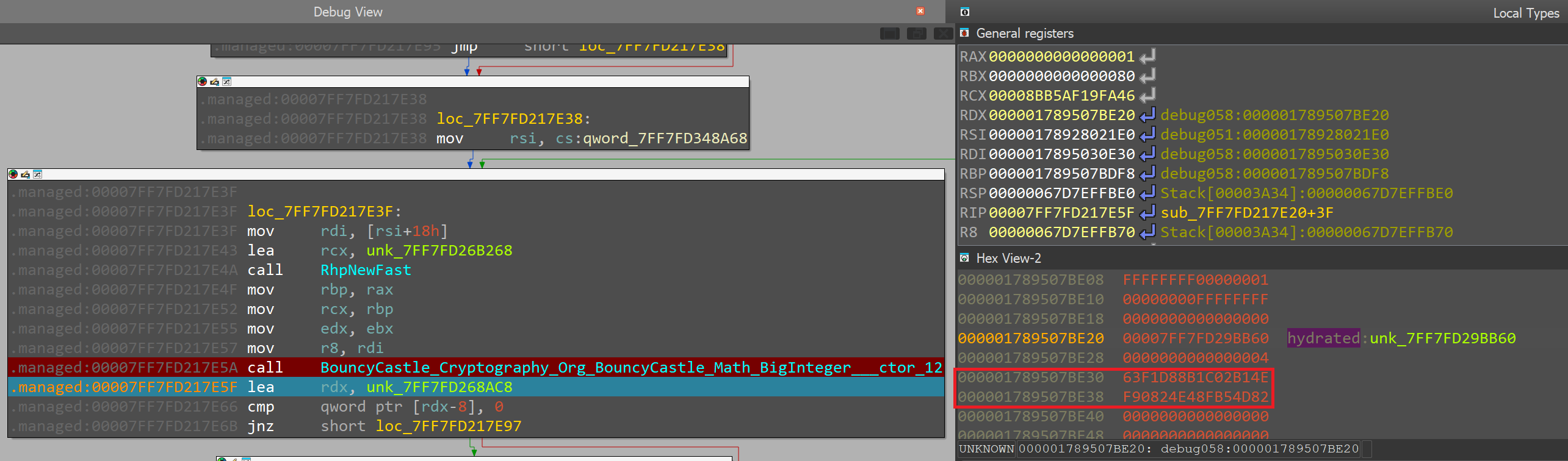
Since this value is generated using a secure PRNG, it's likely used as a private key.
Basically, sub_140107E20 generates a private key, so we'll rename it to generate_private_key. Let's go back to the program main and continue our analysis.
IDA did not identify the target functions called through the indirect calls coming after the function responsible for private key generation, so we'll need to find them ourselves. Similar to what we have done before, after analyzing each function and trying to find patterns in BouncyCastle, I was able to find the following functions:
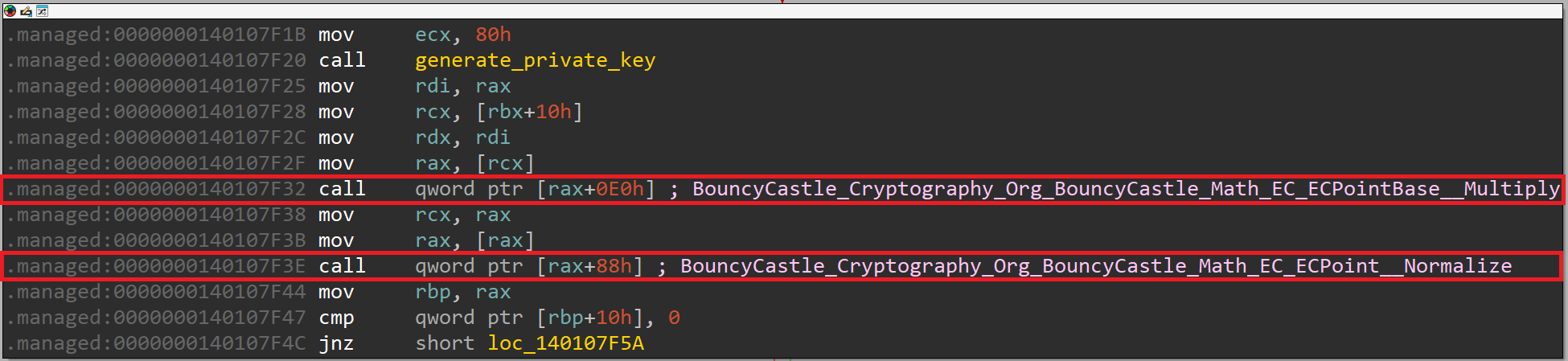
These two functions are used as a part of following the algorithm to create a public key. The public key is created through multiplying the generator point G by the scalar k (private key). This will produce a point on the same curve.
The C# code so far is similar to the following:
BigInteger p = new BigInteger("c90102faa48f18b5eac1f76bb40a1b9fb0d841712bbe3e5576a7a56976c2baeca47809765283aa078583e1e65172a3fd", 16);
BigInteger a = new BigInteger("a079db08ea2470350c182487b50f7707dd46a58a1d160ff79297dcc9bfad6cfc96a81c4a97564118a40331fe0fc1327f", 16);
BigInteger b = new BigInteger("9f939c02a7bd7fc263a4cce416f4c575f28d0c1315c4f0c282fca6709a5f9f7f9c251c9eede9eb1baa31602167fa5380", 16);
BigInteger gx = new BigInteger("087b5fe3ae6dcfb0e074b40f6208c8f6de4f4f0679d6933796d3b9bd659704fb85452f041fff14cf0e9aa7e45544f9d8", 16);
BigInteger gy = new BigInteger("127425c1d330ed537663e87459eaa1b1b53edfe305f6a79b184b3180033aab190eb9aa003e02e9dbf6d593c5e3b08182", 16);
FpCurve curve = new FpCurve(p, a, b);
var G = curve.CreatePoint(gx, gy);
SecureRandom random = new SecureRandom();
BigInteger privatekey = new BigInteger(128, random);
ECPoint publickey = G.Multiply(privateKey).Normalize();
You can display the public key with:
Console.WriteLine("Public Key:");
Console.WriteLine("X: " + publickey.XCoord.ToBigInteger().ToString(16));
Console.WriteLine("Y: " + publickey.YCoord.ToBigInteger().ToString(16));
Next, we have the following block:
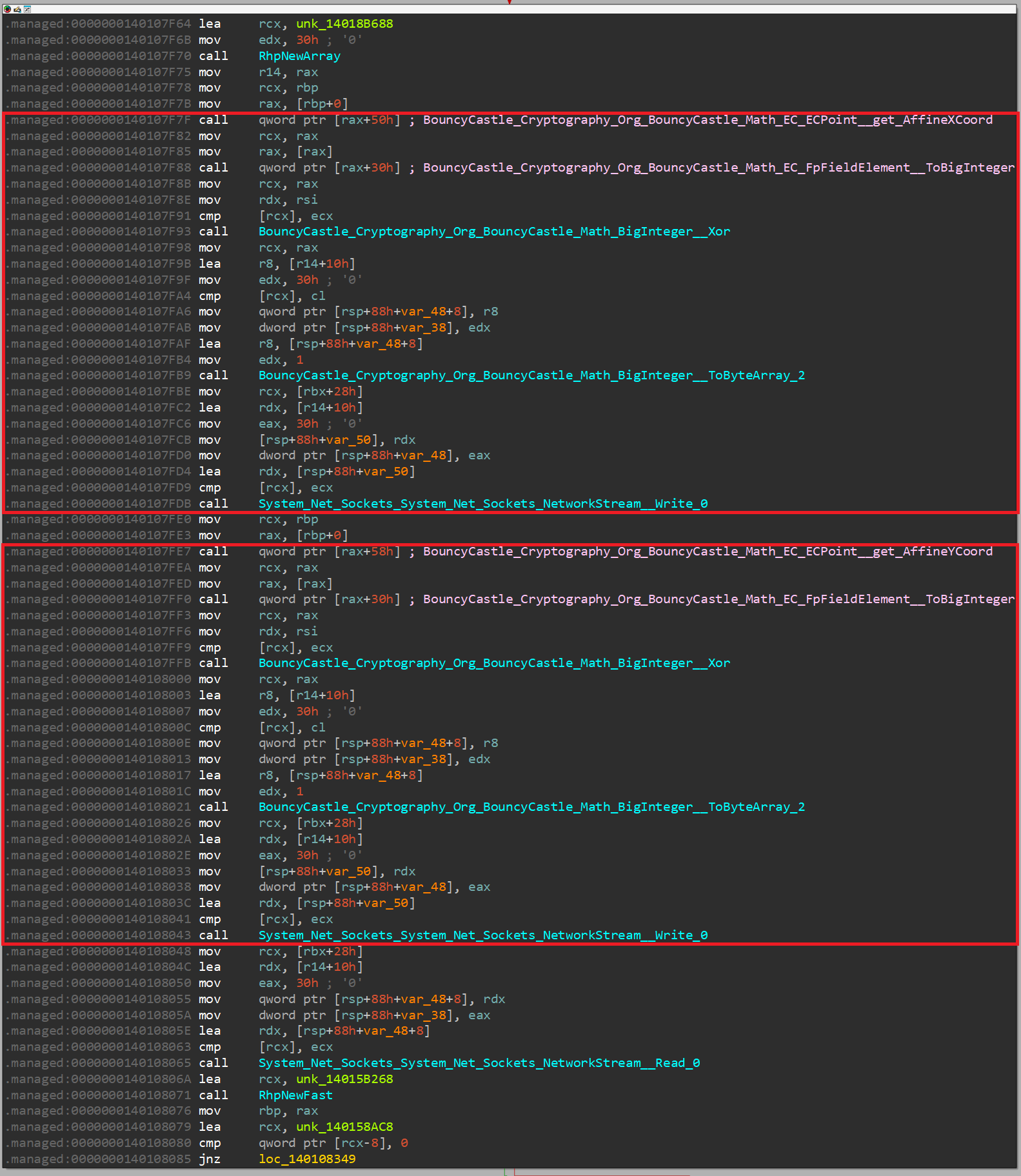
As discussed earlier, I identified the functions (listed as comments) through the same way discussed earlier. The code shows that the X and Y coordinates of the resulting point publickey are being XORed, converted to byte array, and then sent through the socket. We finally have come to know what exactly those values sent by the client in the PCAP file! Let's figure out what they are exactly XORed with.
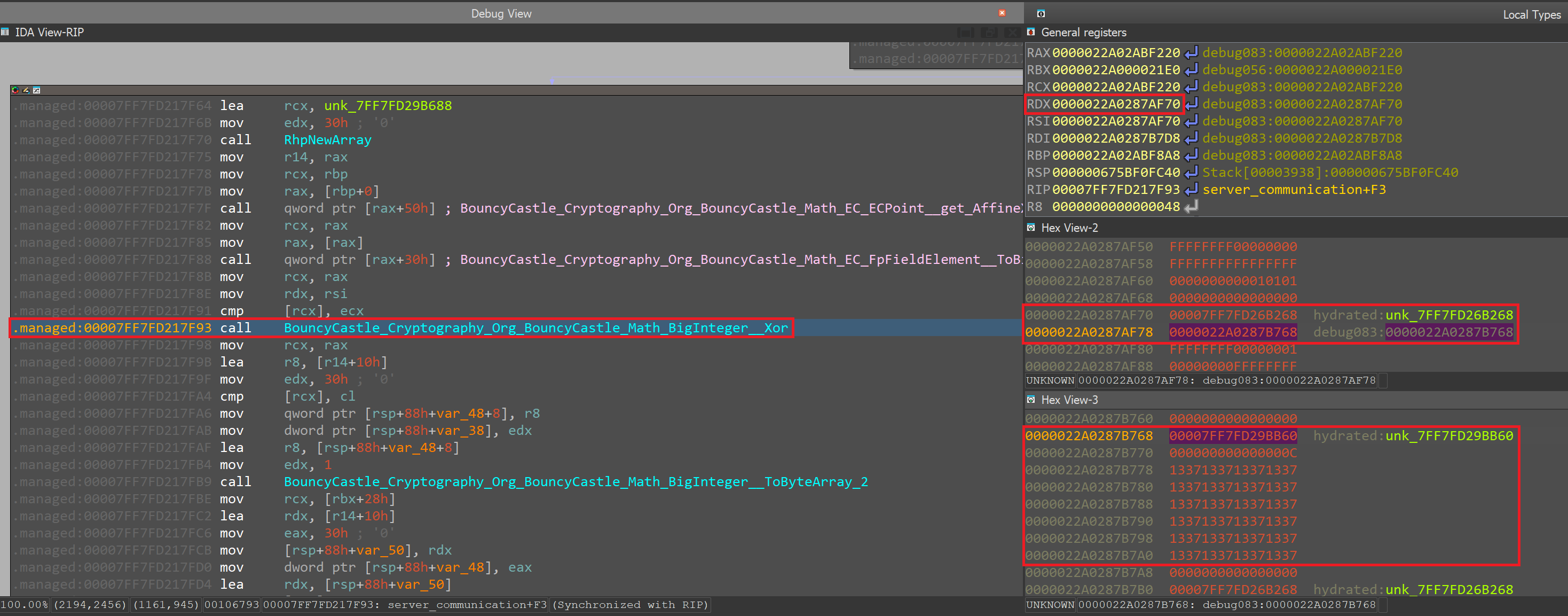
As shown, the X coordinate (and Y as well) is XORed with the 1337 BigInteger we have identified earlier before it's sent to the server.
Next, the program expects to receive two buffers each is 0x30 (48) bytes long, and then applies the same XORing logic. Once done, it creates a point, and multiplies it by the private key to create the shared secret.
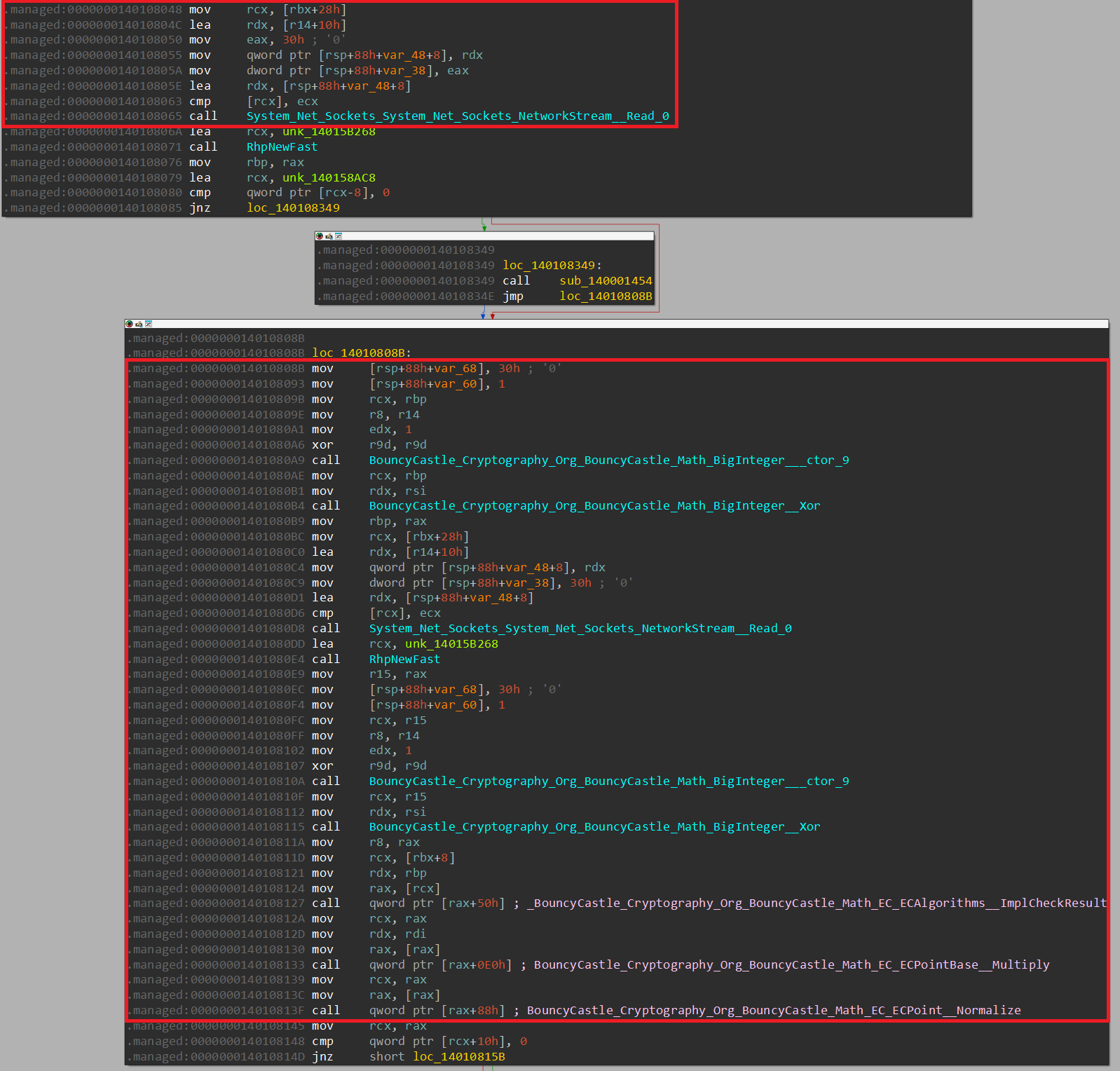
This is done to create a shared secret (point) between the client and the server through the following listed equations:
$$S_{client}:\text{the shared secret that the client calculates.}$$
$$S_{server}:\text{the shared secret that the server calculates.}$$
$$k_{client}:\text{the private key of the client generated through secure random.}$$
$$k_{server}:\text{the private key of the server generated through secure random (assumption).}$$
$$S_{client} = k_{client} \cdot (k_{server} \cdot G)$$
$$S_{client} = (k_{client} \cdot k_{server}) \cdot G$$
The same applies to the server:
$$S_{server} = k_{server} \cdot (k_{client} \cdot G)$$
$$S_{server} = (k_{server} \cdot k_{client}) \cdot G$$
Once the shared key is computed, the next block gets the X coordinate, converts it to byte array, and then calls the function sub_1401074F0:
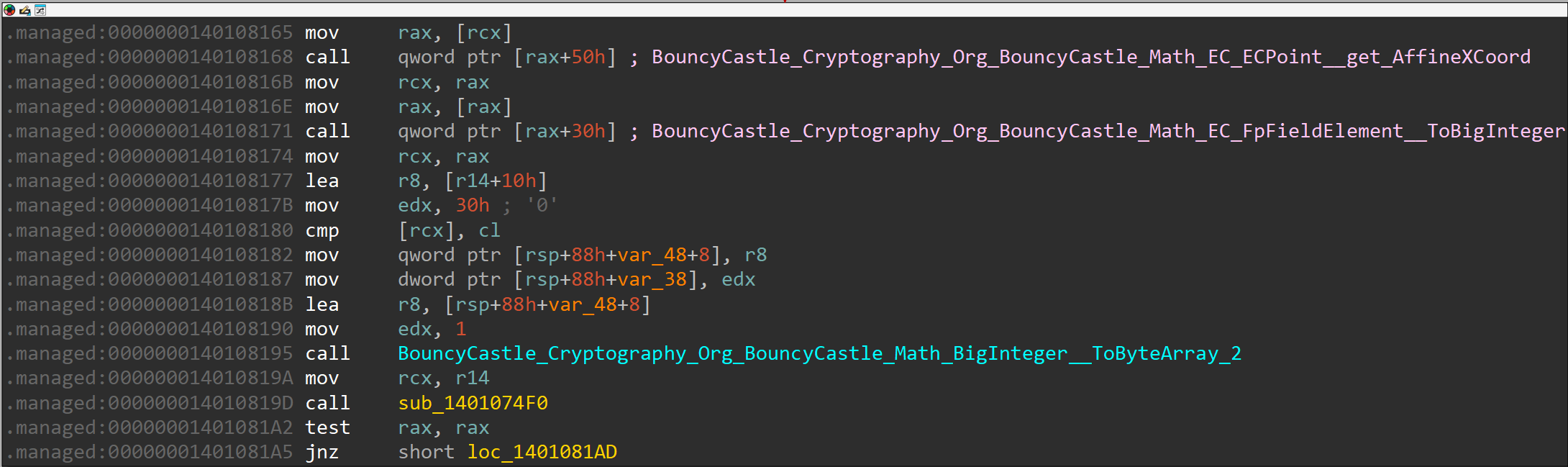
Let's look at what sub_1401074F0 does:
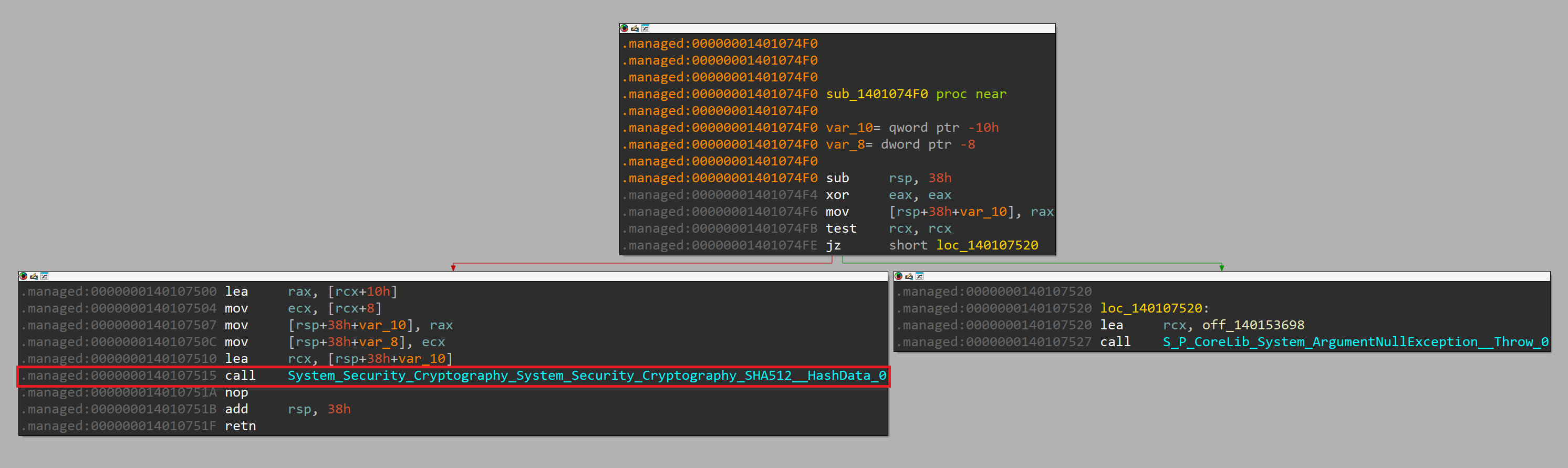
Based on IDA, the function sub_1401074F0 calculates the SHA512 hash of the extracted X coordinate of the shared secret (point).
Next, we notice a call to BouncyCastle_Cryptography_Org_BouncyCastle_Crypto_Engines_Salsa20Engine___ctor_0 in the following block:
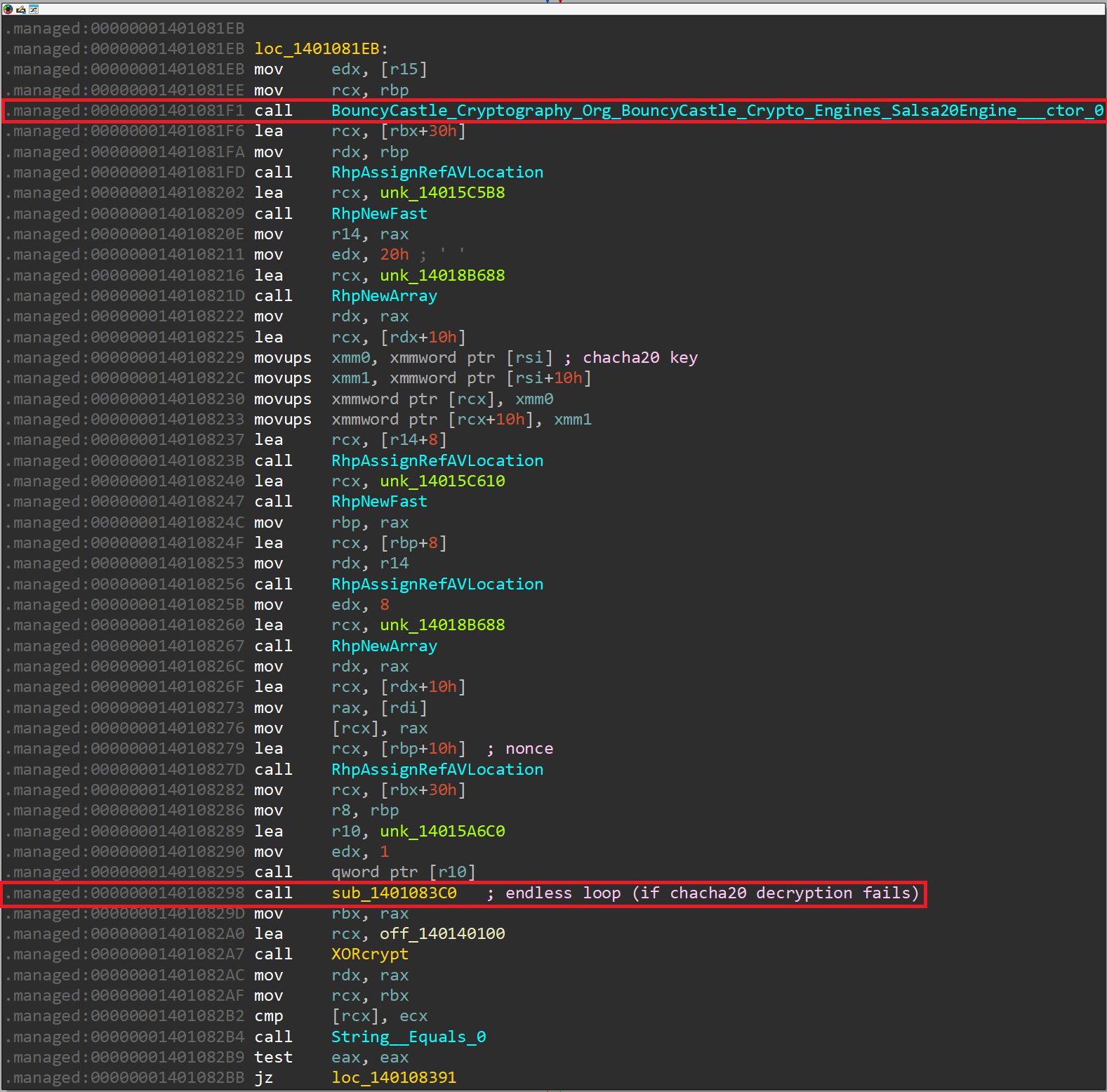
In this block, IDA tells us that there's a call to BouncyCastle_Cryptography_Org_BouncyCastle_Crypto_Engines_Salsa20Engine___ctor_0, but my testing pointed out that the second algorithm used here is ChaCha20 and not Salsa20. My guess is that this happens because in the BouncyCastle project, we can see that ChaChaEngine inherits from Salsa20Engine.
We also notice that the produced SHA512 hash is used to create the ChaCha20 key and nonce. The first 32 bytes of the hash are used for the key, while the following 8 bytes are used as a nonce. The function sub_1401083C0 takes the key and nonce, generates a key stream, and attempts to read one byte at a time. It will enter an endless loop if it does not find a null byte at the end of the decrypted command, which happens in the case that the sent command is not encrypted with a proper or the same key. The internal analysis of the function sub_1401083C0 is left as an exercise for the reader :)
Once the ChaCha20 algorithm is configured on both the client and the server with the same key utilizing elliptic curve properties, the client and server continue exchanging traffic using ChaCha20 as the encryption algorithm.
Now to the cryptography part of this challenge. We know that ChaCha20 key and nonce are built from the SHA512 hash. This hash represents the SHA512 hash of the X coordinate of the shared key (point). Since we know the public key of both the server and client (i.e., the X and Y coordinates from the PCAP file) and all the parameters of the curve, we need to find a way to attack the elliptic curve algorithm.
I'm not a crypto expert myself, but after spending many hours trying to understand the weakness, I stumbled upon an algorithm called Pohlig-Hellman.
Let's try to understand the problem a bit more. We know that:
$$Q = k \cdot G$$
Q is the public key (point). The problem is to figure out k, which is called the discrete logarithm.
This can be achieved through Pohlig Hellman, which works when the order of the group n (the number of elements in the group) has small prime factors.
I stumbled upon the this script which looked very similar to what we have. Although it worked after removing large factors (for computational efficiency), it gave a partial solution that is less than 16 bytes:
from sage.all import *
# Pohlig-Hellman attack
p = 0xc90102faa48f18b5eac1f76bb40a1b9fb0d841712bbe3e5576a7a56976c2baeca47809765283aa078583e1e65172a3fd # Prime modulus
a = 0xa079db08ea2470350c182487b50f7707dd46a58a1d160ff79297dcc9bfad6cfc96a81c4a97564118a40331fe0fc1327f # Curve parameter a
b = 0x9f939c02a7bd7fc263a4cce416f4c575f28d0c1315c4f0c282fca6709a5f9f7f9c251c9eede9eb1baa31602167fa5380 # Curve parameter b
E = EllipticCurve(GF(p), [a, b])
# Define generator and target points
G = E(0x087b5fe3ae6dcfb0e074b40f6208c8f6de4f4f0679d6933796d3b9bd659704fb85452f041fff14cf0e9aa7e45544f9d8, 0x127425c1d330ed537663e87459eaa1b1b53edfe305f6a79b184b3180033aab190eb9aa003e02e9dbf6d593c5e3b08182)
# Q is the client's public point from wireshark after XOR with 1337 bigint
Q = E(0x195b46a760ed5a425dadcab37945867056d3e1a50124fffab78651193cea7758d4d590bed4f5f62d4a291270f1dcf499, 0x357731edebf0745d081033a668b58aaa51fa0b4fc02cd64c7e8668a016f0ec1317fcac24d8ec9f3e75167077561e2a15)
n = G.order()
factors = list(factor(n))
print(f"Factors: {factors}")
print(f"Removing the large factor", factors[-1])
factors = factors[:-1]
print(f"Factors: {factors}")
d = []
subgroup = []
for prime, exponent in factors:
try:
G0 = (n // (prime**exponent)) * G
Q0 = (n // (prime**exponent)) * Q
x = discrete_log(Q0, G0, operation='+')
d.append(x)
subgroup.append(prime**exponent)
print(f"x ≡ {x} mod {prime**exponent}")
except ValueError:
print(f"Discrete log failed for subgroup of order {prime**exponent}")
# Combine with CRT
secret = crt(d, subgroup)
print(f"secret: {hex(secret)}")
(sage) joe@FlareVM:fullspeed$ sage solve.py
Factors: [(35809, 1), (46027, 1), (56369, 1), (57301, 1), (65063, 1), (111659, 1), (113111, 1), (7072010737074051173701300310820071551428959987622994965153676442076542799542912293, 1)]
Removing the large factor (7072010737074051173701300310820071551428959987622994965153676442076542799542912293, 1)
Factors: [(35809, 1), (46027, 1), (56369, 1), (57301, 1), (65063, 1), (111659, 1), (113111, 1)]
x ≡ 11872 mod 35809
x ≡ 42485 mod 46027
x ≡ 12334 mod 56369
x ≡ 45941 mod 57301
x ≡ 27946 mod 65063
x ≡ 43080 mod 111659
x ≡ 57712 mod 113111
secret: 0xc0f9af2dbc735ae5a57cf155b870
As shown, the discovered secret is 14 bytes only. From our analysis, we know that it should be 16 bytes (128 bits).
Since we discarded the large factor, we got a partial solution. Pohlig-Hellman works by breaking n into small factors, but we removed the large prime factor because it's computationally expensive. Without that large prime factor, we only find a partial solution.
To compensate for the skipped prime, we will iteratively test candidates of the form private_key = partial_secret + modulus * i (for i up to n/modulus) and verify if Q = private_key * G. If it is, we display the private key.
The following calculates the correct private key:
from sage.all import *
# Pohlig-Hellman attack
p = 0xc90102faa48f18b5eac1f76bb40a1b9fb0d841712bbe3e5576a7a56976c2baeca47809765283aa078583e1e65172a3fd # Prime modulus
a = 0xa079db08ea2470350c182487b50f7707dd46a58a1d160ff79297dcc9bfad6cfc96a81c4a97564118a40331fe0fc1327f # Curve parameter a
b = 0x9f939c02a7bd7fc263a4cce416f4c575f28d0c1315c4f0c282fca6709a5f9f7f9c251c9eede9eb1baa31602167fa5380 # Curve parameter b
E = EllipticCurve(GF(p), [a, b])
# Define generator and target points
G = E(0x087b5fe3ae6dcfb0e074b40f6208c8f6de4f4f0679d6933796d3b9bd659704fb85452f041fff14cf0e9aa7e45544f9d8, 0x127425c1d330ed537663e87459eaa1b1b53edfe305f6a79b184b3180033aab190eb9aa003e02e9dbf6d593c5e3b08182)
# Q is the client's public point from wireshark after XOR with 1337 bigint
Q = E(0x195b46a760ed5a425dadcab37945867056d3e1a50124fffab78651193cea7758d4d590bed4f5f62d4a291270f1dcf499, 0x357731edebf0745d081033a668b58aaa51fa0b4fc02cd64c7e8668a016f0ec1317fcac24d8ec9f3e75167077561e2a15)
n = G.order()
factors = list(factor(n))
print(f"Factors: {factors}")
print(f"Removing the large factor", factors[-1])
factors = factors[:-1]
print(f"Factors: {factors}")
d = []
subgroup = []
for prime, exponent in factors:
try:
G0 = (n // (prime**exponent)) * G
Q0 = (n // (prime**exponent)) * Q
x = discrete_log(Q0, G0, operation='+')
d.append(x)
subgroup.append(prime**exponent)
except ValueError:
print(f"Discrete log failed for subgroup of order {prime**exponent}")
# Combine with CRT
partial_secret = crt(d, subgroup)
print(f"Partial secret: {hex(partial_secret)}")
# Brute-force refinement
modulus = prod(subgroup)
for i in range(n // modulus):
private_key = partial_secret + modulus * i
if private_key * G == Q:
break
print(f"Private key: {hex(private_key)}")
(sage) joe@FlareVM:fullspeed$ sage solve.py
Factors: [(35809, 1), (46027, 1), (56369, 1), (57301, 1), (65063, 1), (111659, 1), (113111, 1), (7072010737074051173701300310820071551428959987622994965153676442076542799542912293, 1)]
Removing the large factor (7072010737074051173701300310820071551428959987622994965153676442076542799542912293, 1)
Factors: [(35809, 1), (46027, 1), (56369, 1), (57301, 1), (65063, 1), (111659, 1), (113111, 1)]
Partial secret: 0xc0f9af2dbc735ae5a57cf155b870
Private key: 0x7ed85751e7131b5eaf5592718bef79a9
Awesome! Now that we have the private key, we can just multiply by the server's public key (point), get X coordinate, calculate the SHA512 of it, get Chacha20 key, and decrypt everything!
The following is the code that does all of this:
from sage.all import *
from hashlib import sha512
from Crypto.Cipher import ChaCha20
import struct
def pohlig_hellman_and_bruteforce(E, G, Q):
n = G.order()
factors = list(factor(n))
print(f"Factors: {factors}")
print(f"Removing the large factor", factors[-1])
factors = factors[:-1]
print(f"Factors: {factors}")
d = []
subgroup = []
for prime, exponent in factors:
try:
G0 = (n // (prime**exponent)) * G
Q0 = (n // (prime**exponent)) * Q
x = discrete_log(Q0, G0, operation='+')
d.append(x)
subgroup.append(prime**exponent)
except ValueError:
print(f"Discrete log failed for subgroup of order {prime**exponent}")
# Combine with CRT
partial_secret = crt(d, subgroup)
print(f"Partial secret: {hex(partial_secret)}")
# Brute-force refinement
modulus = prod(subgroup)
for i in range(n // modulus):
private_key = partial_secret + modulus * i
if private_key * G == Q:
break
print(f"Private key: {hex(private_key)}")
return private_key
# Function to decrypt the stream of bytes using ChaCha20
def chacha20_decrypt(ciphertext, key, nonce):
# Create a ChaCha20 cipher object with the given key and nonce
cipher = ChaCha20.new(key=key, nonce=nonce)
# Decrypt the ciphertext
plaintext = cipher.decrypt(ciphertext)
return plaintext
def flip_endianess(data_hex):
""" Unpacks the hexadecimal string to bytes, swaps endianess, and repacks to a byte array. """
if type(data_hex) == str:
data = bytes.fromhex(data_hex)
else:
data = data_hex
swapped = bytearray()
# Ensure we process every 4-byte chunk correctly.
for i in range(0, len(data), 4):
swapped.extend(struct.pack('<I', struct.unpack('>I', data[i:i+4])[0]))
return swapped
def xor(data, key = "133713371337133713371337133713371337133713371337133713371337133713371337133713371337133713371337"):
""" Performs XOR between hexadecimal data and a key. """
data = int.from_bytes(flip_endianess(data), 'big')
key = int.from_bytes(flip_endianess(key), 'big')
result = data ^ key
# Determine the appropriate length for the output.
result_length = (result.bit_length() + 7) // 8
return result.to_bytes(result_length, 'big')
def exchange_crypt(data):
result = xor(data)
data = flip_endianess(xor(data).hex())
return bytes(data)
def main():
# Pohlig-Hellman attack
p = 0xc90102faa48f18b5eac1f76bb40a1b9fb0d841712bbe3e5576a7a56976c2baeca47809765283aa078583e1e65172a3fd # Prime modulus
a = 0xa079db08ea2470350c182487b50f7707dd46a58a1d160ff79297dcc9bfad6cfc96a81c4a97564118a40331fe0fc1327f # Curve parameter a
b = 0x9f939c02a7bd7fc263a4cce416f4c575f28d0c1315c4f0c282fca6709a5f9f7f9c251c9eede9eb1baa31602167fa5380 # Curve parameter b
# Generator point
gx = 0x087b5fe3ae6dcfb0e074b40f6208c8f6de4f4f0679d6933796d3b9bd659704fb85452f041fff14cf0e9aa7e45544f9d8
gy = 0x127425c1d330ed537663e87459eaa1b1b53edfe305f6a79b184b3180033aab190eb9aa003e02e9dbf6d593c5e3b08182
# Public XY coordinates of the client (from wireshark)
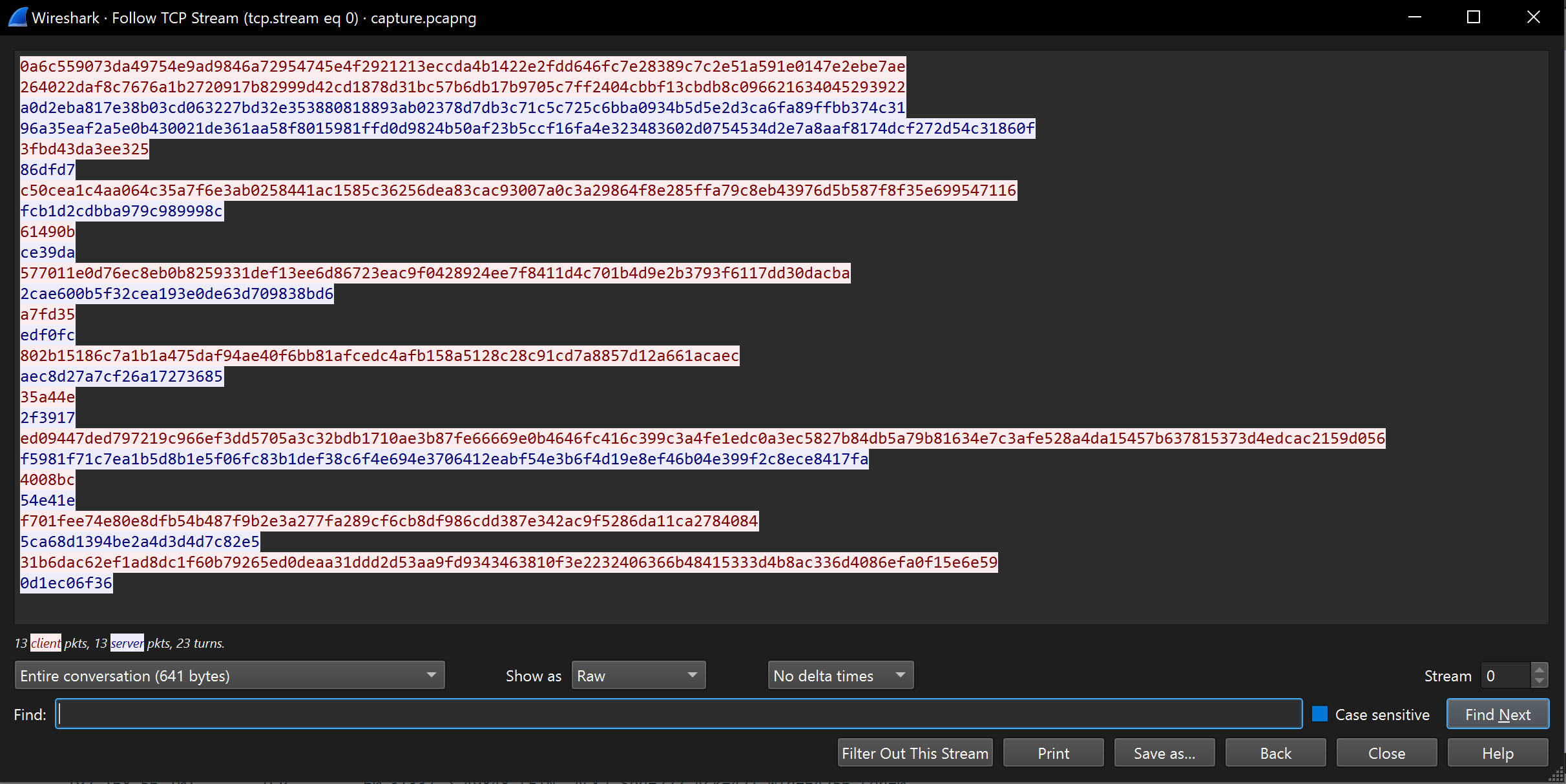
cPx = int.from_bytes(exchange_crypt("0a6c559073da49754e9ad9846a72954745e4f2921213eccda4b1422e2fdd646fc7e28389c7c2e51a591e0147e2ebe7ae"), "big")
cPy = int.from_bytes(exchange_crypt("264022daf8c7676a1b2720917b82999d42cd1878d31bc57b6db17b9705c7ff2404cbbf13cbdb8c096621634045293922"), "big")
# Public XY coordinates of the server (from wireshark)
sPx = int.from_bytes(exchange_crypt("a0d2eba817e38b03cd063227bd32e353880818893ab02378d7db3c71c5c725c6bba0934b5d5e2d3ca6fa89ffbb374c31"), "big")
sPy = int.from_bytes(exchange_crypt("96a35eaf2a5e0b430021de361aa58f8015981ffd0d9824b50af23b5ccf16fa4e323483602d0754534d2e7a8aaf8174dc"), "big")
# Entire encrypted data (from wireshark)
encrypted_data = "f272d54c31860f3fbd43da3ee32586dfd7c50cea1c4aa064c35a7f6e3ab0258441ac1585c36256dea83cac93007a0c3a29864f8e285ffa79c8eb43976d5b587f8f35e699547116fcb1d2cdbba979c989998c61490bce39da577011e0d76ec8eb0b8259331def13ee6d86723eac9f0428924ee7f8411d4c701b4d9e2b3793f6117dd30dacba2cae600b5f32cea193e0de63d709838bd6a7fd35edf0fc802b15186c7a1b1a475daf94ae40f6bb81afcedc4afb158a5128c28c91cd7a8857d12a661acaecaec8d27a7cf26a1727368535a44e2f3917ed09447ded797219c966ef3dd5705a3c32bdb1710ae3b87fe66669e0b4646fc416c399c3a4fe1edc0a3ec5827b84db5a79b81634e7c3afe528a4da15457b637815373d4edcac2159d056f5981f71c7ea1b5d8b1e5f06fc83b1def38c6f4e694e3706412eabf54e3b6f4d19e8ef46b04e399f2c8ece8417fa4008bc54e41ef701fee74e80e8dfb54b487f9b2e3a277fa289cf6cb8df986cdd387e342ac9f5286da11ca27840845ca68d1394be2a4d3d4d7c82e531b6dac62ef1ad8dc1f60b79265ed0deaa31ddd2d53aa9fd9343463810f3e2232406366b48415333d4b8ac336d4086efa0f15e6e590d1ec06f36"
E = EllipticCurve(GF(p), [a, b])
# Generator point
G = E(gx, gy)
# Target points
Q_c = E(cPx, cPy)
Q_s = E(sPx, sPy)
client_private_key = pohlig_hellman_and_bruteforce(E, G, Q_c)
# Shared secret point
shared_point = Q_s * client_private_key
x_cord, _ = shared_point.xy()
x_cord_hash = sha512(x_cord.to_bytes()).digest()
chacha20_key = x_cord_hash[:32]
chacha20_nonce = x_cord_hash[32:40]
print("chacha20_key:", chacha20_key.hex())
print("chacha20_nonce:", chacha20_nonce.hex())
decrypted_data = chacha20_decrypt(bytes.fromhex(encrypted_data), chacha20_key, chacha20_nonce)
print(decrypted_data) # base64_decode(b"RDBudF9VNWVfeTB1cl9Pd25fQ3VSdjNzQGZsYXJlLW9uLmNvbQ==") = "D0nt_U5e_y0ur_Own_CuRv3s@flare-on.com"
if __name__ == "__main__":
main()

Finally! The flag is D0nt_U5e_y0ur_Own_CuRv3s@flare-on.com
Hope you enjoyed it, and if not... well, at least your keyboard survived the debugging session! Happy hacking! 😄
